Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
a) Tính góc tạo bởi hai đường thẳng AC’ và A’B.
b) Gọi M, N, P lần lượt là trung điểm của các cạnh A’B’, BC, DD’. Chứng minh rằng AC’ vuông góc với mp(MNP).

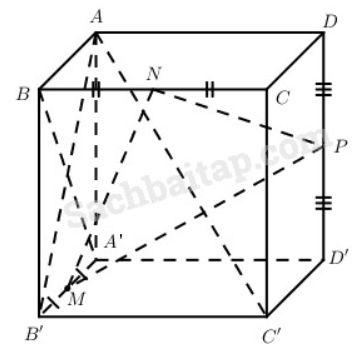
a) Ta có \(C’B’ \bot \left( {ABB’A’} \right),B’A \bot A’B\) nên \(A’B \bot AC’\) (định lí ba đường vuông góc).
Vậy góc giữa AC’ và A’B bằng 90°.
b) Ta có
Advertisements (Quảng cáo)
\(\eqalign{ & N{P^2} = N{C^2} + C{{\rm{D}}^2} + D{P^2} \cr & = {{{a^2}} \over 4} + {a^2} + {{{a^2}} \over 4} = {{3{{\rm{a}}^2}} \over 2} \cr} \)
Tương tự ta cũng có \(M{N^2} = M{P^2} = {{3{{\rm{a}}^2}} \over 2}\)
Vậy MNP là tam giác đều.
Mặt khác:
\(\eqalign{ & A{N^2} = A{P^2} = A{M^2} = {{5{{\rm{a}}^2}} \over 4} \cr & C'{N^2} + C'{P^2} = C'{M^2} = {{5{{\rm{a}}^2}} \over 4} \cr} \)
Từ đó \(AC’ \bot \left( {MNP} \right)\).
