Câu 6 trang 221 Sách bài tập Hình học 11 Nâng cao. Từ đó nếu ta gọi D là trung điểm của đoạn thẳng MM’ thì \(\overrightarrow {C{\rm{D}}} = \overrightarrow {BA} \), tức D là điểm xác định. ÔN TẬP CUỐI NĂM - HÌNH HỌC
Cho ba điểm A, B, C. Gọi ĐA, ĐB, ĐC là các phép đối xứng tâm có tâm lần lượt là A, B và C. Chứng minh rằng hợp thành của ba phép đối xứng tâm nói trên là một phép đối xứng tâm.
Advertisements (Quảng cáo)
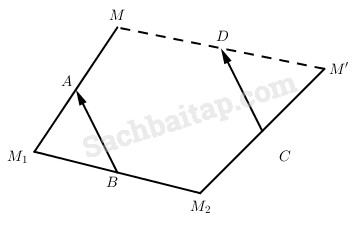
Gọi F là phép hợp thành của ba phép đối xứng ĐA, ĐB và ĐC. Gọi M là điểm bất kì sao cho M1 = ĐA(M), M2 = ĐB(M1), M’ = ĐC(M2), có nghĩa là các điểm A, B, C lần lượt là trung điểm các đoạn \(M{M_1},{M_1}{M_2},{M_2}M’\)
Từ đó nếu ta gọi D là trung điểm của đoạn thẳng MM’ thì \(\overrightarrow {C{\rm{D}}} = \overrightarrow {BA} \), tức D là điểm xác định không phụ thuộc vào M. Theo định nghĩa của phép hợp thành F thì F biến điểm M thành điểm M’. Vì D là trung điểm của MM’ nên F là phép đối xứng tâm với tâm là D.