Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi cạnh a, \(\widehat A = {60^0}\), góc của đường chéo A’C và mặt phẳng đáy bằng 600.
a) Tính đường cao của hình hộp đó.
b) Tìm đường vuông góc chung của A’C và BB’. Tính khoảng cách giữa hai đường thẳng đó.

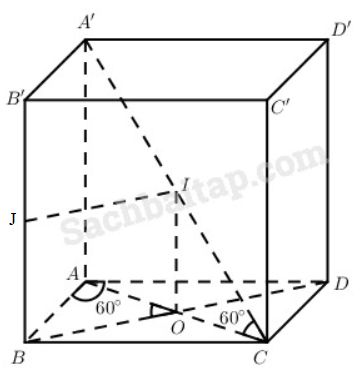
a) Dễ thấy \(\widehat {A’CA} = {60^0}\).
Do ABCD là hình thoi cạnh a và \(\widehat A = {60^0}\) nên \(AC = a\sqrt 3 \).
Đường cao của hình hộp ABCD.A’B’C’D’ chính là A’A. Mặt khác
Advertisements (Quảng cáo)
\(A’A = AC\tan \widehat {A’CA} = a\sqrt 3 \tan {60^0} = 3{\rm{a}}\) .
b) Ta có BB’ // (A’AC) và \(BO \bot \left( {A’AC} \right)\) với O là tâm của hình thoi ABCD (giao điểm của hai đường chéo).
Kẻ OI // AA’ và kẻ IJ // BO thì dễ dàng chứng minh được IJ là đường vuông góc chung của BB’ và A’C. Khoảng cách giữa hai đường thẳng BB’ và A’C chính là BO. Mặt khác \(BO = {a \over 2}\).
Vậy \(d\left( {BB’;A’C} \right) = {a \over 2}.\)
Chú ý: Có thể tìm thấy đường vuông góc chung của BB’ và A’C và IJ (I, J lần lượt là trung điểm của A’C và BB’) bằng cách xét tứ diện A’B’BC có:
\(\eqalign{ & A’B’ = BC = a, \cr & A’B = B’C = \sqrt {{a^2} + BB{‘^2}} \cr} \)
