Cho hình chóp S.ABCD có đáy là hình tam giác vuông tại C, CA = b, CB = a, cạnh SA = h vuông góc với đáy. Gọi D là trung điểm của cạnh AB. Tính:
a) Góc giữa hai đường thẳng AC và SD;
b) Khoảng cách giữa hai đường thẳng AC và SD;
c) Khoảng cách giữa hai đường thẳng BC và SD.

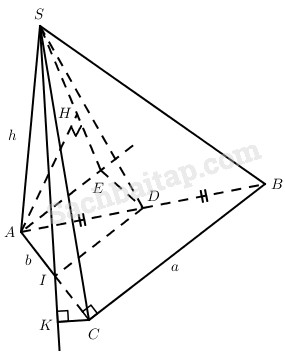
a) Gọi E là giao điểm của đường thẳng qua D, song song với AC và đường thẳng qua A, song song với BC thì AED và SED là hai tam giác vuông tại E, do đó \(\widehat {S{\rm{D}}E}\) là góc giữa SD và AC.
Đặt \(\widehat {S{\rm{D}}E} = \alpha \) thì
\(\tan \alpha = {{SE} \over {E{\rm{D}}}} = {{\sqrt {{h^2} + {{{a^2}} \over 4}} } \over {{b \over 2}}}\)
hay \(\tan \alpha = {{\sqrt {{a^2} + 4{h^2}} } \over b}\)
b) Vì AC // (SDE) nên \(d\left( {AC;S{\rm{D}}} \right) = d\left( {A;\left( {S{\rm{D}}E} \right)} \right)\).
Do \(DE \bot \left( {SA{\rm{E}}} \right)\) nên \(\left( {S{\rm{D}}E} \right) \bot \left( {SA{\rm{E}}} \right)\).
Advertisements (Quảng cáo)
Vậy nếu kẻ đường cao AH của tam giác vuông SAE thì AH là khoảng cách giữa AC và SD.
Ta có \(AH = {{AS.AE} \over {SE}} = {{h.{a \over 2}} \over {{1 \over 2}\sqrt {{a^2} + 4{h^2}} }} = {{ah} \over {\sqrt {{a^2} + 4{h^2}} }}\)
Vậy khoảng cách giữa AC và SD là \(AH = {{ah} \over {\sqrt {{a^2} + 4{h^2}} }}\).
c) Gọi I là trung điểm của AC thì BC // (SDI).
Do đó \(d\left( {BC;S{\rm{D}}} \right) = d\left( {C;\left( {S{\rm{D}}I} \right)} \right)\)
Ta có \(DI \bot \left( {SAC} \right)\) nên \(\left( {S{\rm{D}}I} \right) \bot \left( {SAC} \right)\).
Vậy khi kẻ đường cao CK của tam giác SIC thì CK là khoảng cách phải tìm.
Ta có \({S_{SIC}} = {{bh} \over 4},SI = {1 \over 2}\sqrt {4{h^2} + {b^2}} \)
nên \(CK = {{{{bh} \over 2}} \over {{1 \over 2}\sqrt {4{h^2} + {b^2}} }}\)
hay \(CK = {{bh} \over {\sqrt {4{h^2} + {b^2}} }}\)
Vậy khoảng cách giữac BC và SD bằng \({{bh} \over {\sqrt {4{h^2} + {b^2}} }}\).
