Cho hình chữ nhật ABCD có AB = a, AD = b. Gọi S là điểm sao cho SA vuông góc với mp(ABC) và SA = h (h > 0). Trên cạnh CD lấy điểm M bất kì, đặt CM = x (0 ≤ x ≤a).
a) Tính diện tích tam giác SBM theo a, b, h, x.
b) Tính khoảng cách từ điểm A đến mp(SBM) khi M là trung điểm của CD.
c) Gọi hình chiếu của điểm A và điểm D trên mp(SBM) lần lượt là A1 và D1. Chứng minh rằng khi M thay đổi trên CD thì các điểm A1 và D1 thuộc một đường tròn cố định. Tính bán kính của mỗi đường tròn đó.

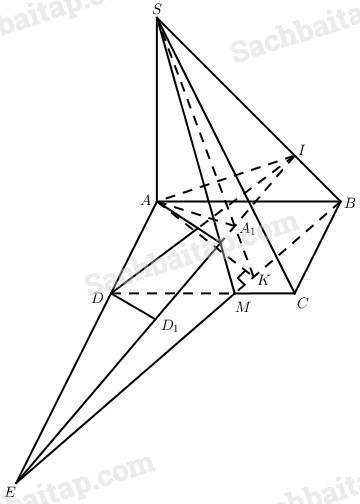
a) Kẻ \(AK \bot MB\), do \(SA \bot \left( {ABC} \right)\) nên \(SK \bot MB\) (định lí ba đường vuông góc).
Vậy \({S_{SBM}} = {1 \over 2}BM.SK\)
Mặt khác \(BM = \sqrt {{b^2} + {x^2}} \) và \(AK.MB = 2{{\rm{S}}_{AMB}} = ab\)
tức là \(AK = {{ab} \over {\sqrt {{b^2} + {x^2}} }}\)
Từ đó
\(\eqalign{ & S{K^2} = S{A^2} + A{K^2} = {h^2} + {{{a^2}{b^2}} \over {{b^2} + {x^2}}} \cr & = {{{a^2}{b^2} + {b^2}{h^2} + {h^2}{x^2}} \over {{b^2} + {x^2}}} \cr} \)
Vậy \({S_{SBM}} = {1 \over 2}\sqrt {{a^2}{b^2} + {b^2}{h^2} + {h^2}{x^2}} \)
b) Với A1 là hình chiếu A trên SK, dễ thấy \(A{A_1} \bot \left( {SBM} \right)\).
Từ đó \(A{A_1}.SK = SA.AK\)
suy ra \(A{A_1} = {{SA.AK} \over {SK}}\)
hay
Advertisements (Quảng cáo)
\(\eqalign{ & A{A_1} = {{h.{{ab} \over {\sqrt {{b^2} + {x^2}} }}} \over {{{\sqrt {{a^2}{b^2} + {b^2}{h^2} + {h^2}{x^2}} } \over {\sqrt {{b^2} + {x^2}} }}}} \cr & = {{abh} \over {\sqrt {{a^2}{b^2} + {b^2}{h^2} + {h^2}{x^2}} }} \cr} \)
Khi trung điểm DC thì \(x = {a \over 2}\) nên
\(A{A_1} = {{2abh} \over {\sqrt {4{a^2}{b^2} + 4{b^2}{h^2} + {a^2}{h^2}} }}\)
c) Vì \(A{A_1} \bot \left( {SMB} \right)\) nên \(A{A_1} \bot SB\) mặt khác \(A{\rm{D}} \bot SB\), từ đó \(mp\left( {A{\rm{D}}{A_1}} \right) \bot SB.\)
Gọi giao điểm của SB với mp(ADA1) là I thì \(AI \bot SB\), từ đó I là điểm cố định và mp(ADA1) cố định.
Như vậy, điểm A1 nhìn AI cố định dưới góc vuông và A1 thuộc mặt phẳng cố định (ADI), tức là A1 thuộc đường tròn đường kính AI trong mp(ADI).
Bán kính của đường tròn đó bằng \({{AI} \over 2}\) mà
\(AI.SB = SA.AB\)
hay \(AI = {{ah} \over {\sqrt {{a^2} + {h^2}} }}\)
Vậy bán kính của đường tròn trên bằng \({{ah} \over {2\sqrt {{a^2} + {h^2}} }}\).
Vì D1 là hình chiếu của D trên mp(SBM) nên DD1 // AA1 và dễ thất D1 thuộc đường thẳng A1I.
Như vậy, D1 thuộc mp(ADI) và D1 nhìn DI dưới góc vuông, tức là điểm D1 thuộc đường tròn đường kính DI trong mp(ADI). Bán kính của đường tròn đó \({{DI} \over 2}\).
Mặt khác
\(\eqalign{ & D{I^2} = D{A^2} + A{I^2} \cr & = {b^2} + {{{a^2}{h^2}} \over {{a^2} + {h^2}}} \cr & = {{{a^2}{b^2} + {b^2}{h^2} + {a^2}{h^2}} \over {{a^2} + {h^2}}} \cr} \)
Từ đó, bán kính của đường tròn đó là
\({1 \over 2}\sqrt {{{{a^2}{b^2} + {a^2}{h^2} + {b^2}{h^2}} \over {{a^2} + {h^2}}}} \)
