Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, AD = b; cạnh bên SA vuông góc với mặt phẳng đáy, AS = 2a. Gọi M là điểm bất kì trên cạnh AS, đặt \(AM = x\left( {0 \le x \le 2{\rm{a}}} \right)\).
a) Thiết diện của hình chóp S.ABCD khi cắt bởi mp(MBC) là hình gì? Tính diện tích thiết diện.
b) Tính khoảng cách từ điểm S đến mp(MBC) ứng với mỗi vị trí của M.

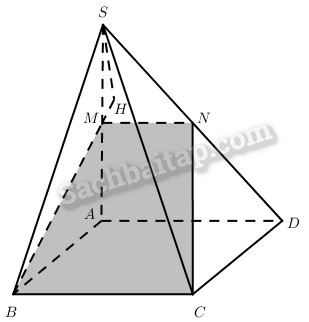
a) Vì \(BC//SA{\rm{D}},M \in mp\left( {SA{\rm{D}}} \right) \cap mp\left( {MBC} \right)\)
nên \(mp\left( {MBC} \right) \cap \left( {SA{\rm{D}}} \right) = MN\)
mà \(MN//BC\left( {N \in S{\rm{D}}} \right)\).
Như vậy BMNC là hình thang.
Mặt khác \(BC \bot \left( {SAB} \right)\) nên \(BC \bot BM\).
Vậy BMNC là hình thang vuông.
Do đó thiết diện của hình chóp S.ABCD khi cắt bởi mp(MBC) nói chung là hình thang vuông.
Advertisements (Quảng cáo)
Khi x = 0 thì thiết diện là hình chữ nhật ABCD, và khi x = 2a thì thiết diện là tam giác SBC.
Ta có
\(\eqalign{ & {S_{BMNC}} = {1 \over 2}\left( {BC + MN} \right).BM \cr & B{M^2} = {a^2} + {x^2} \cr} \)
hay \(BM = \sqrt {{a^2} + {x^2}} \)
\({{MN} \over {A{\rm{D}}}} = {{SM} \over {SA}} = {{2{\rm{a}} - x} \over {2{\rm{a}}}}\), từ đó \(MN = b.{{2{\rm{a}} - x} \over {2{\rm{a}}}}\).
Từ đó
\(\eqalign{ & {S_{BMNC}} = {1 \over 2}\left( {b + b.{{2{\rm{a}} - x} \over {2{\rm{a}}}}} \right).\sqrt {{a^2} + {x^2}} \cr & = {b \over {4{\rm{a}}}}\left( {4{\rm{a}} - x} \right)\sqrt {{a^2} + {x^2}} \cr} \)
b) Do \(\left( {BMNC} \right) \bot \left( {SAB} \right)\) nên khi kẻ SH vuông góc với đường thẳng \(BM\left( {H \in BM} \right)\) thì \(SH \bot \left( {BMNC} \right)\).
Khoảng cách từ S đến mp(BCM) là SH. Dễ thấy
\(SH.BM = 2{{\rm{S}}_{SBM}} = 2.{1 \over 2}a\left( {2{\rm{a}} - x} \right)\)
Vậy \(SH = {{a\left( {2{\rm{a}} - x} \right)} \over {\sqrt {{a^2} + {x^2}} }}\)
