Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi I là điểm thuộc AB; đặt \(AI = x\left( {0 < x < a} \right)\).
a) Khi góc giữa hai đường thẳng AC’ và DI bằng 60°, hãy xác định vj trí của điểm I.
b) Tính theo a và x diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng (B’DI). Tìm x để diện tích ấy là nhỏ nhấ.
c) Tính khoảng cách từ đến mặt phẳng (B’DI) theo a và x.

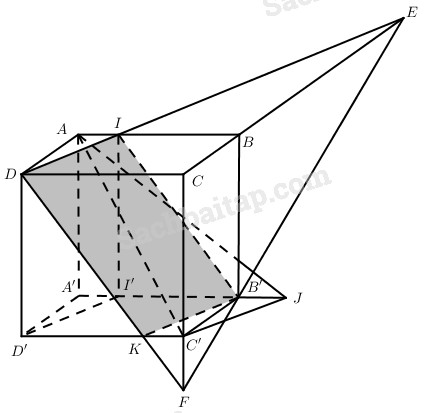
a) Cách 1.
Đặt α là góc giữa DI và AC’ thì
\(\eqalign{ & \cos \alpha = {{\left| {\overrightarrow {DI} .\overrightarrow {AC’} } \right|} \over {\left| {\overrightarrow {DI} } \right|.\left| {\overrightarrow {AC’} } \right|}} \cr & = {{\left( {\overrightarrow {DA} + \overrightarrow {AI} } \right)\left( {\overrightarrow {AD} + \overrightarrow {AB} + \overrightarrow {AA’} } \right)} \over {\left| {\overrightarrow {DI} } \right|.\left| {\overrightarrow {AC’} } \right|}} \cr & = {{\left| { - {a^2} + xa} \right|} \over {\sqrt {{a^2} + {x^2}.a\sqrt 3 } }} = {{\left| { - a + x} \right|} \over {\sqrt 3 .\sqrt {{a^2} + {x^2}} }} \cr} \)
Khi ấy \(\alpha = {60^0}\) khi và chỉ khi
\(\eqalign{ & {{\left| { - a + x} \right|} \over {\sqrt 3 .\sqrt {{a^2} + {x^2}} }} = {1 \over 2} \cr & \Leftrightarrow {x^2} - 8ax + {a^2} = 0 \cr & \Leftrightarrow x = a\left( {4 - \sqrt {15} } \right)\,\,\,\left( {vì\,\,0 < x < a} \right) \cr} \)
Hệ thức trên xác định vị trí điểm I.
Cách 2.
Kẻ \(II’//AA’\left( {I’ \in A’B’} \right),C’J//D’I’\) (I’ thuộc đường thẳng A’B’) thì \(\widehat {AC’J}\) hoặc \({180^0} - \widehat {AC’J}\) là góc giữa hai đường thẳng AC’ và DI với B’J = x.
Do giả thiết góc giữa hai đường thẳng AC’ và DI bằng 60° nên \(\widehat {AC’J} = {60^0}\) hoặc 120°.
Ta có :
\(\eqalign{ & A{J^2} = AA{‘^2} + A'{J^2} = {a^2} + {\left( {a + x} \right)^2} \cr & AC{‘^2} = 3{a^2},C'{J^2} = {a^2} + {x^2} \cr} \)
- Trường hơp \(\widehat {AC’J} = {60^0}\), ta có
\(A{J^2} = AC{‘^2} + C'{J^2} - 2AC’.C’J.{1 \over 2}\)
hay
\(\eqalign{& {a^2} + {\left( {a + x} \right)^2} \cr & = 3{a^2} + {a^2} + {x^2} - 2a\sqrt 3 .\sqrt {{a^2} + {x^2}.{1 \over 2}} \cr & \Leftrightarrow {x^2} - 8ax + {a^2} = 0 \cr & \Rightarrow x = \left( {4 - \sqrt {15} } \right)a\,\,\left( {vì\,0 < x < a} \right) \cr}\)
Trường hợp \(\widehat {AC’J} = {120^0}\), ta có
\(\eqalign{& {a^2} + {\left( {a + x} \right)^2} \cr & = 3{{\rm{a}}^2} + {a^2} + {x^2} + 2{\rm{a}}\sqrt 3 .\sqrt {{a^2} + {x^2}} .{1 \over 2} \cr & \Leftrightarrow 2ax = 2{a^2} + a\sqrt 3 .\sqrt {{a^2} + {x^2}} \cr & \Leftrightarrow 2\left( {x - a} \right) = \sqrt 3 .\sqrt {{a^2} + {x^2}} \cr} \)
Advertisements (Quảng cáo)
Điều này không xảy ra vì 0 < x < a.
Vậy khi \(x = \left( {4 - \sqrt {15} } \right)a\) thì góc giữa DI và AC’ bằng 60°.
b) Gọi
\(\eqalign{ & E = DI \cap CB \cr & F = B’E \cap CC’ \cr & K = DF \cap D’C’ \cr} \)
thì thiết diện của hình lập phương khi cắt bởi mp(B’DI) là tứ giác DIB’K.
Dễ thấy đó là hình bình hành
\({S_{DIB’K}} = 2{{\rm{S}}_{B’I{\rm{D}}}}\)
\(= 2.{1 \over 2}\sqrt {{{\overrightarrow {IB’} }^2}.{{\overrightarrow {I{\rm{D}}} }^2} - {{\left( {\overrightarrow {IB’} .\overrightarrow {I{\rm{D}}} } \right)}^2}} \)
Mặt khác \({\overrightarrow {I{\rm{D}}} ^2}.{\overrightarrow {IB’} ^2} = \left( {{a^2} + {x^2}} \right)\left[ {{a^2} + {{\left( {a - x} \right)}^2}} \right]\)
và \(\eqalign{ & {\left( {\overrightarrow {I{\rm{D}}} .\overrightarrow {IB’} } \right)^2} = {\left[ {\left( {\overrightarrow {IA} + \overrightarrow {A{\rm{D}}} } \right)\left( {\overrightarrow {IB} + \overrightarrow {BB’} } \right)} \right]^2} \cr & = {\left( {\overrightarrow {IA} .\overrightarrow {IB} } \right)^2} = {\left[ { - x{{\left( {a - x} \right)}^2}} \right]^2} = {x^2}{\left( {a - x} \right)^2} \cr} \)
Từ đó
\(\eqalign{ & {S_{DIB’K}} = \sqrt {{a^4} + {a^2}{x^2} + {a^2}{{\left( {a - x} \right)}^2}} \cr & = a\sqrt {{a^2} + {x^2} + {{\left( {a - x} \right)}^2}} \cr} \)
Dễ thấy \({S_{DIB’K}}\) đạt giá trị nhỏ nhất khi \(x = {a \over 2}\) .
c) Gọi khoảng cách từ C đến mp(B’ID), do tứ diện CDEF có CD, CE , CF đôi một vuông góc nên
\({1 \over {{h^2}}} = {1 \over {C{{\rm{D}}^2}}} + {1 \over {C{E^2}}} + {1 \over {C{F^2}}}\).
Mặt khác do AD // BE nên \({a \over {BE}} = {x \over {a - x}}\).
từ đó \(BE = {{a\left( {a - x} \right)} \over x}\)
và \(CE = a + {{a\left( {a - x} \right)} \over x} = {{{a^2}} \over x}\).
Tương tự như trên, ta có \(C’F = {{ax} \over {a - x}}\) từ đó
\(CF = a + {{ax} \over {a - x}} = {{{a^2}} \over {a - x}}\).
Như vậy \({1 \over {{h^2}}} = {1 \over {{a^2}}} + {{{x^2}} \over {{a^4}}} + {{{{\left( {a - x} \right)}^2}} \over {{a^4}}}\)
do vậy \(h = {{{a^2}} \over {\sqrt {{a^2} + {x^2} + {{\left( {a - x} \right)}^2}} }}\)
