Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ có đường cao bằng h. Góc giữa mặt phẳng chứa mặt bên và mặt đáy bằng α. Góc giữa đường thẳng A’C và mặt đáy bằng β. Tính:
a) Cạnh đáy, trung đoạn của hình chóp cụt;
b) Diện tích xung quanh của hình chóp cụt đó.

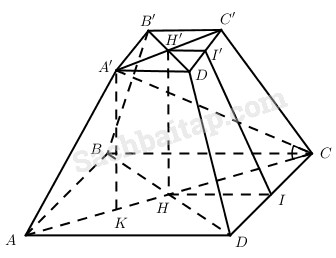
Gọi H, H’ lần lượt là tâm hai đáy ABCD, A’B’C’D’. I, I’ lần lượt là trung điểm của CD, C’D’ thì \(HH’ = h;\widehat {A’CA} = \beta ;\widehat {I’IH} = \alpha .\)
Dễ thấy \(II’ = {h \over {\sin \alpha }}\) .
Kí hiệu độ dài cạnh của các đáy ABCD, A’B’C’D’ lần lượt là x, y (x > y).
Ta có
\(\eqalign{ & {{x - y} \over 2} = h\cot \alpha \cr & \Leftrightarrow x - y = 2h\cot \alpha \,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr} \)
Advertisements (Quảng cáo)
Kẻ A’K // HH thì A’K = HH’ = h và
\(\eqalign{ & KC = A’K\cot \beta \,\, \cr & hay\,\,x\sqrt 2 - {{x\sqrt 2 - y\sqrt 2 } \over 2} = h\cot \beta \cr} \)
Từ đó
\(\eqalign{ & {{\left( {x + y} \right)\sqrt 2 } \over 2} = h\cot \beta \cr & \Leftrightarrow x + y = \sqrt 2 h\cot \beta \,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \cr} \)
Từ (1) và (2) ta có \(x = {h \over 2}\left( {\sqrt 2 \cot \beta + 2\cot \alpha } \right)\)
\(y = {h \over 2}\left( {\sqrt 2 \cot \beta - 2\cot \alpha } \right)\)
(điều kiện \(\sqrt 2 \cot \beta - 2\cot \alpha > 0\) )
b)
\(\eqalign{ & {S_{xq}} = 4.{1 \over 2}\left( {x + y} \right)II’ \cr & = 2\sqrt 2 h\cot \beta .{h \over {\sin \alpha }} \cr & = {{2\sqrt 2 {h^2}\cot \beta } \over {\sin \alpha }}. \cr} \)
