Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ cạnh đáy bằng a, cạnh bên \(a\sqrt 6 \). Xét đường thẳng ∆ đi qua điểm A và song song với BD. Gọi (P) là mặt phẳng qua ∆ và điểm C’.
a) Thiết diện của hình lăng trụ đã cho khi cắt bởi mp(P) là hình gì? Tính diện tích thiết diện.
b) Tính góc giữa mp(P) và mp(ABCD).

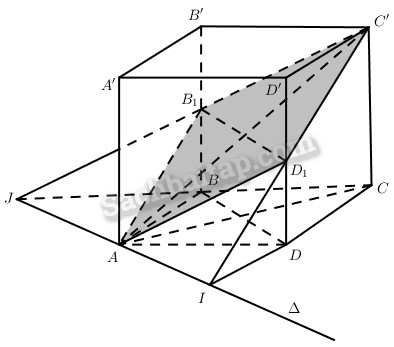
a) Gọi \(I = C{\rm{D}} \cap \Delta ,J = BC \cap \Delta \),
\({B_1} = C’J \cap BB’,{D_1} = C’I \cap {\rm{DD}}’\)
thì thiết diện thu được \(A{B_1}C'{D_1}\).
Dễ thấy \(A{B_1}C'{D_1}\) là hình bình hành và B1, D1 lần lượt là trung điểm của BB’, DD’.
Từ đó \(A{{\rm{D}}_1} = {D_1}C’\)
Do đó thiết diện \(A{B_1}C'{D_1}\) là hình thoi.
Advertisements (Quảng cáo)
\(\eqalign{ & {S_{A{B_1}C'{D_1}}} = {1 \over 2}{B_1}{D_1},AC’ \cr & {B_1}{D_1} = B{\rm{D}} = a\sqrt 2 \cr & AC{‘^2} = A{C^2} + CC{‘^2} = 2{{\rm{a}}^2} + 6{{\rm{a}}^2} = 8{{\rm{a}}^2} \cr & \Rightarrow AC’ = 2{\rm{a}}\sqrt 2 \cr} \)
Vậy \({S_{A{B_1}C'{D_1}}} = {1 \over 2}a\sqrt 2 .2{\rm{a}}\sqrt 2 = 2{{\rm{a}}^2}.\)
b) Ta có \(AC \bot B{\rm{D}}\) mà ∆ // BD nên \(AC \bot \Delta \).
Mặt khác \(C’C \bot \left( {ABC{\rm{D}}} \right)\) nên \(AC’ \bot \Delta \) (định lí ba đường vuông góc).
Vậy \(\widehat {C’AC}\) là góc giữa mp(P) và mp(ABCD).
Ta có \(\tan \widehat {C’AC} = {{CC’} \over {AC}} = {{a\sqrt 6 } \over {a\sqrt 2 }} = \sqrt 3 \), từ đó \(\widehat {C’AC} = {60^0}\)
Chú ý. Cũng có thể tính góc giữa mp(P) và mp(ABCD) bởi công thức
\({S_{ABC{\rm{D}}}} = {S_{A{B_1}C'{D_1}}} = 2{{\rm{a}}^2}\)
mà \({S_{ABC{\rm{D}}}} = {a^2},{S_{A{B_1}C'{D_1}}} = 2{{\rm{a}}^2}\)
tức là \(\cos \varphi = {1 \over 2}\,\,hay\,\,\varphi = {60^0}\).
