Cho hình chóp đều S.ABC. Chứng minh. Bài 3.28 trang 153 Sách bài tập (SBT) Hình học 11 - Bài 4. Hai mặt phẳng vuông góc
Cho hình chóp đều S.ABC. Chứng minh
a) Mỗi cạnh bên của hình chóp đó vuông góc với cạnh đối diện ;
b) Mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.
Advertisements (Quảng cáo)
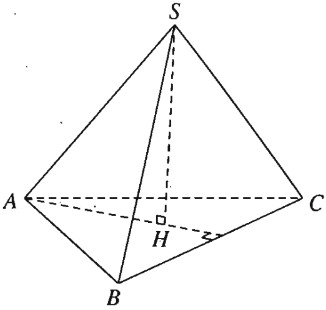
a) Vì S.ABC là hình chóp đều nên ∆ABC là tam giác đều và có SA = SB = SC. Do đó khi ta vẽ \(SH \bot \left( {ABC} \right)\) thì H là trọng tâm của tam giác đều ABC và ta có \(AH \bot BC\). Theo định lí ba đường vuông góc ta có \(SA \bot BC\).
Chứng minh tương tự ta có \(SB \bot AC\) và \(SC \bot AB\)
b) Vì \(BC \bot AH\) và \(BC \bot SH\) nên \(BC \bot \left( {SAH} \right)\)
Chứng minh tương tự ta có \(CA \bot \left( {SBH} \right)\) và \(AB \bot \left( {SCH} \right)\).