Hoạt động 1
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) có đồ thị như Hình 1.
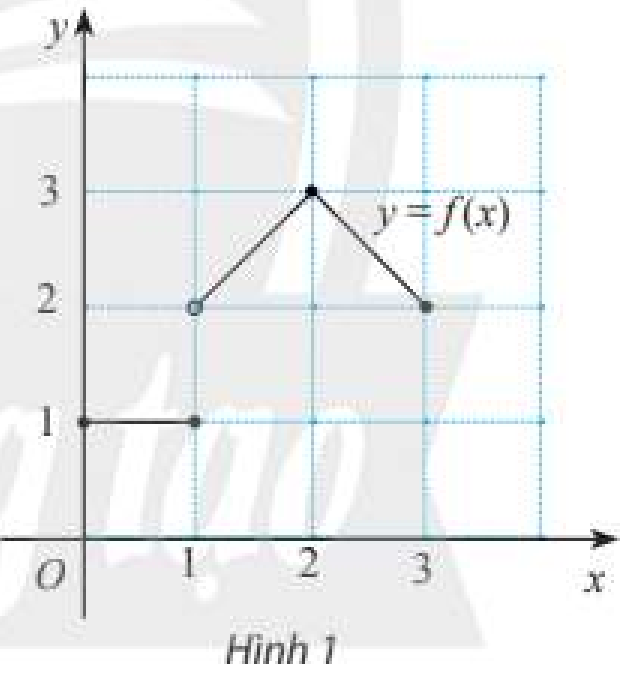
Tại mỗi điểm \({x_0} = 1\) và \({x_0} = 2\), có tồn tại giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không? Nếu có, giới hạn đó có bằng \(f\left( {{x_0}} \right)\) không?

Bước 1: Tính các giới hạn một bên \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right),\mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\).
Bước 2: So sánh \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right),\mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\)
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right) = L\) thì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\).
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) \ne \mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\) thì không tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\).

• \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {1 + x} \right) = 1 + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} 1 = 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
• \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {5 - x} \right) = 5 - 2 = 3\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {1 + x} \right) = 1 + 2 = 3\).
Vì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 3\).
Ta có: \(f\left( 2 \right) = 1 + 2 = 3\).
Vậy \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\).
Thực hành 1
Advertisements (Quảng cáo)
Xét tính liên tục của hàm số:
a) \(f\left( x \right) = 1 - {x^2}\) tại điểm \({x_0} = 3\);
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 1}&{khi\,\,x > 1}\\{ - x}&{khi\,\,x \le 1}\end{array}} \right.\) tại điểm \({x_0} = 1\).

Bước 1: Kiểm tra \({x_0}\) thuộc tập xác định. Tính \(f\left( {{x_0}} \right)\).
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) (nếu có).
Bước 3: Kết luận:
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) thì hàm số liên tục tại điểm \({x_0}\).
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right)\) hoặc không tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) thì hàm số không liên tục tại điểm \({x_0}\).

a) \(f\left( 3 \right) = 1 - {3^2} = 1 - 9 = - 8\).
\(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \left( {1 - {x^2}} \right) = 1 - {3^2} = 1 - 9 = - 8\).
Vì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right) = - 8\) nên hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 3\).
b) \(f\left( 1 \right) = - 1\).
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} + 1} \right) = {1^2} + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - x} \right) = - 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\)
Vậy hàm số không liên tục tại điểm \({x_0} = 1\).
