
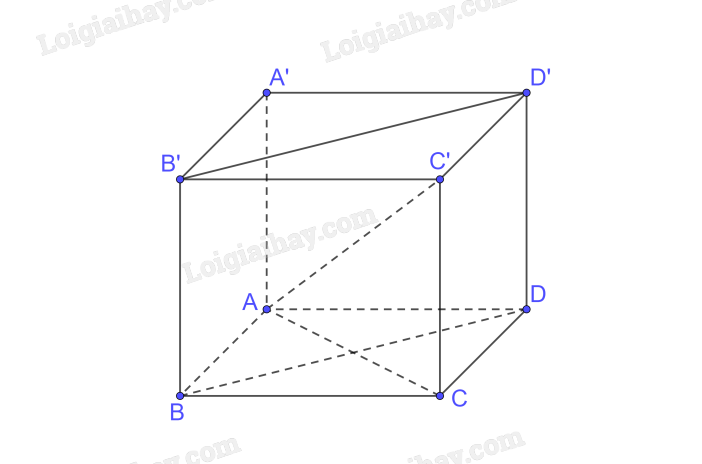
Cho hình hộp chữ nhật ABCD. A’B’C’D’.
a) Chứng minh rằng (BDD′B′) \( \bot \) (ABCD).
b) Xác định hình chiếu của AC′ trên mặt phẳng (ABCD).
c) Cho AB = a, BC = b, CC′ = c. Tính AC′.

Hai mặt phẳng được gọi là vuông góc nếu một đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.

Advertisements (Quảng cáo)
a) Ta có \(BB’ \bot \left( {ABCD} \right);BB’ \subset \left( {BDD’B’} \right) \Rightarrow \left( {BDD’B’} \right) \bot \left( {ABCD} \right)\)
b) A là hình chiếu của A trên (ABCD)
C là hình chiếu của C’ trên (ABCD) do \(CC’ \bot \left( {ABCD} \right)\)
\( \Rightarrow \) AC là hình chiếu của AC’ trên (ABCD)
c) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \)
Xét tam giác AC’C vuông tại C có
\(A{C’^2} = C{C’^2} + A{C^2} = {c^2} + {a^2} + {b^2} \Rightarrow A’C = \sqrt {{a^2} + {b^2} + {c^2}} \)
