Trên mặt đất phẳng, người ta dựng một cây cột AB có chiều dài bằng \(10\;{\rm{m}}\) và tạo với mặt đất góc \({80^0}\). Tại một thời điểm dưới ánh sáng mặt trời, bóng BC của cây cột trên mặt đất dài \(12\;{\rm{m}}\) vào tạo với cây cột một góc bằng \({120^0}\) (tức là \(\widehat {ABC} = {120^0}\)). Tính góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên.
Định lý cosin: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
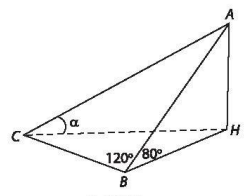
Góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên là \(\widehat {ACH}\)
Xét tam giác ABC có
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC} = {10^2} + {12^2} - 2.10.12.\cos {120^0} = 364\\ \Rightarrow AC = 2\sqrt {91} \left( m \right)\end{array}\)
Gọi H là hình chiếu của A trên mặt đất
Xét tam giác ABH vuông tại H có
\(AH = 10.\sin {80^0}\)
Xét tam giác ACH vuông tại H có
\(\sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{{10\sin {{80}^0}}}{{2\sqrt {91} }} \Rightarrow \widehat {ACH} \approx {31^0}\)
Vậy góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên khoảng 310.