
Cho hình hộp \(ABCD.A’B’C’D’\) có độ dài tất cả các cạnh bằng \(a,AA’ \bot (ABCD)\) và \(\widehat {BAD} = {60^0}\).
a) Tính thể tích của khối hộp \(ABCD.A’B’C’D’\).
b) Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( {A’BD} \right)\).

- Thể tích của khối hộp bằng tích của diện tích một mặt và chiều cao của khối hộp ứng với mặt đó.
- Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P).

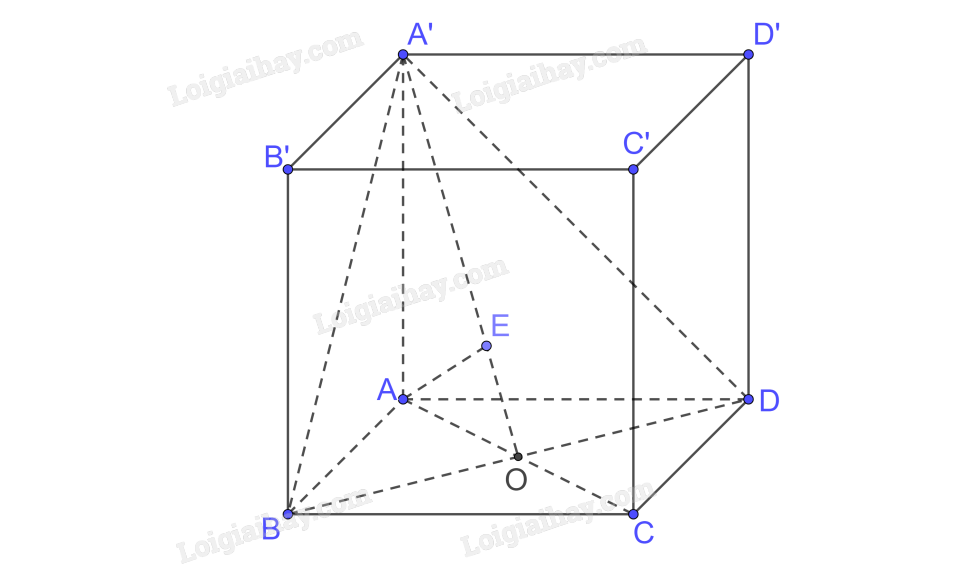
a) Diện tích tam giác ABD bằng diện tích tam giác BCD vì chung đáy BD và chiều cao AO = OC (ABCD là hình thoi)
Diện tích tam giác ABD: \({S_{ABD}} = \frac{1}{2}AB.AD.\sin \widehat {BAD} = \frac{1}{2}a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Rightarrow S = 2{S_{ABD}} = \frac{{{a^2}\sqrt 3 }}{2}\)
Advertisements (Quảng cáo)
Thể tích khối hộp là \(V = AA’.{S_{ABCD}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}\)
b) Gọi \(AC \cap BD = \left\{ O \right\}\)
Ta có \(AA’ \bot BD,AO \bot BD \Rightarrow BD \bot \left( {A’AO} \right);BD \subset \left( {A’BD} \right) \Rightarrow \left( {A’AO} \right) \bot \left( {A’BD} \right)\)
\(\left( {A’AO} \right) \cap \left( {A’BD} \right) = A’O\)
Trong (A’AO) kẻ \(AE \bot A’O\)
\( \Rightarrow AE \bot \left( {A’BD} \right) \Rightarrow d\left( {A,\left( {A’BD} \right)} \right) = AE\)
Xét tam giác ABD có AB = AD và \(\widehat {BAD} = {60^0}\) nên tam giác ABD đều
\( \Rightarrow OA = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác AOA’ vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{A{{A’}^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{7}{{3{a^2}}} \Rightarrow AE = \frac{{a\sqrt {21} }}{7}\)
Vậy \(d\left( {A,\left( {A’BD} \right)} \right) = \frac{{a\sqrt {21} }}{7}\)
