
Cho tứ diện ABCD có tam giác ABC cân tại \(A\), tam giác BCD cân tại \(D\). Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng \(BC \bot (AID)\).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng \(AH \bot (BCD)\).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.

- Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
- Hai mặt phẳng vuông góc nếu trong mặt phẳng này có một đường thẳng vuông góc vào giao tuyến thì đường thẳng đó vuông góc với mặt phẳng còn lại.
- Đường thẳng \(\Delta \) cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.

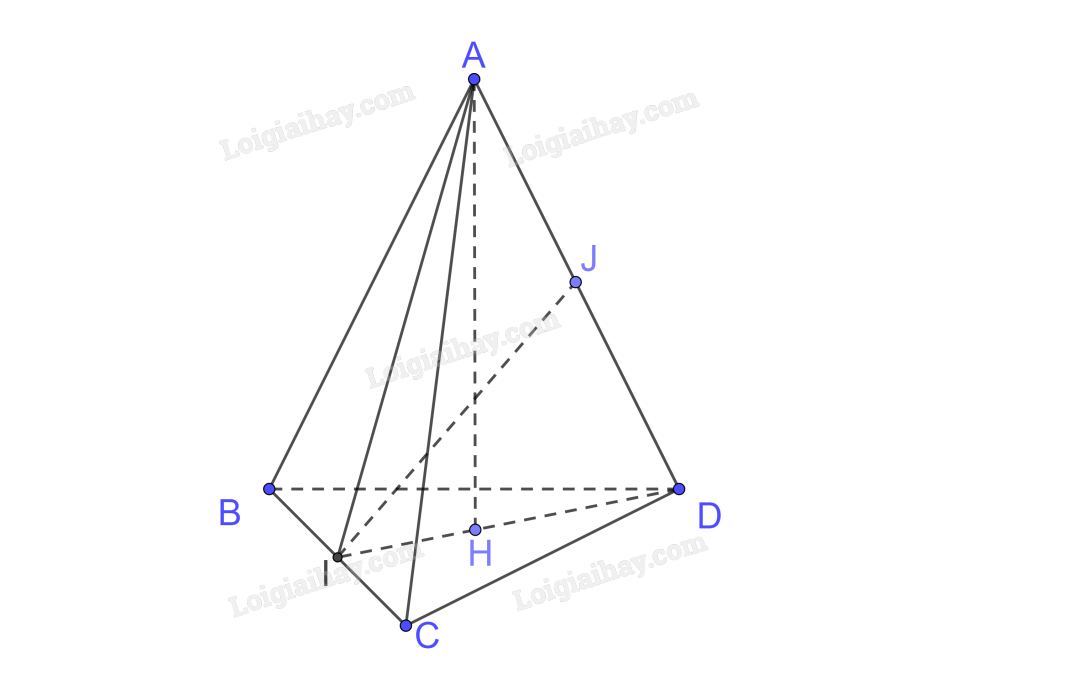
a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
Advertisements (Quảng cáo)
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC
