
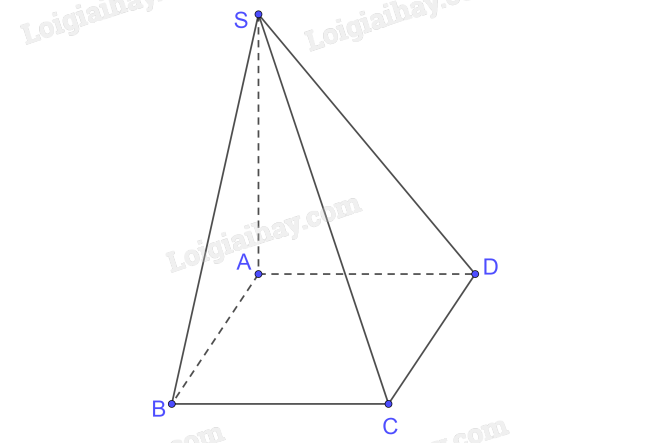
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA \( \bot \) (ABCD). Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông.

- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
- Định nghĩa đường thẳng vuông góc mặt phẳng.

\(\begin{array}{l}\left. \begin{array}{l} + )BC \bot AB\left( {hcn\,\,ABCD} \right)\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AB \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right);SB \subset \left( {SAB} \right) \Rightarrow BC \bot SB\\\left. \begin{array}{l} + )CD \bot AD\left( {hcn\,\,ABCD} \right)\\CD \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AD \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow CD \bot SD\end{array}\)
Xét tam giác SAB có
\(SA \bot AB\left( {SA \bot \left( {ABCD} \right)} \right)\)
Advertisements (Quảng cáo)
\( \Rightarrow \) Tam giác SAB vuông tại A
Xét tam giác SBC có
\(SB \bot BC\)
\( \Rightarrow \) Tam giác SBC vuông tại B
Xét tam giác SCD có
\(SD \bot CD\)
\( \Rightarrow \) Tam giác SCD vuông tại D
Xét tam giác SAD có
\(SA \bot AD\left( {SA \bot \left( {ABCD} \right)} \right)\)
\( \Rightarrow \) Tam giác SAD vuông tại A
