Hoạt động1
Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a’ cùng vuông góc với (P), hai đường thẳng b, b’ cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a,b) và (a’, b’).
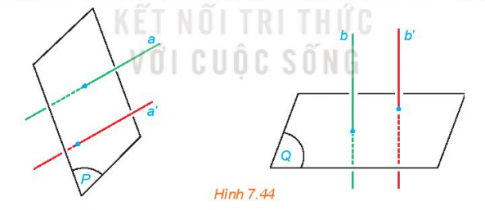

- Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- Nếu b // b’ thì (a, b) = (a, b’).

Vì hai đường thẳng a, a’ cùng vuông góc với (P), hai đường thẳng b, b’ cùng vuông góc với (Q) nên a // a’, b // b’
Vậy (a,b) = (a’, b’)
Câu hỏi1
Góc giữa hai mặt phẳng bằng 00 khi nào, khác 00 khi nào?

Vị trí tương đối 2 mặt phẳng

Advertisements (Quảng cáo)
Góc giữa hai mặt phẳng
+) bằng 00 khi trùng nhau
+) khác 00 khi giao nhau
Luyện tập1
Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO \( \bot \) (ABCD). Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông.

Sử dụng nhận xét trang 45 để xác định góc giữa 2 mặt phẳng.

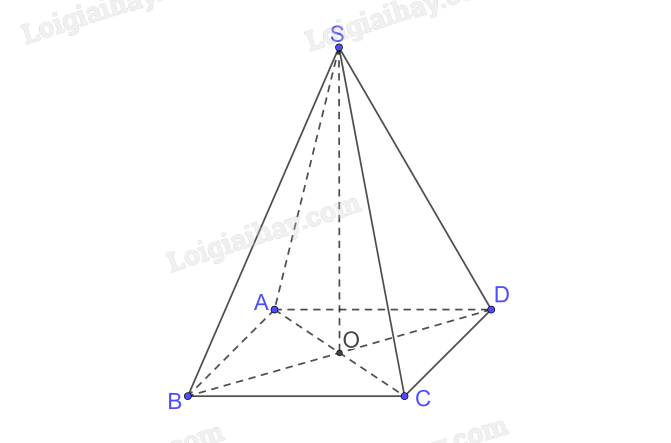
\(\left. \begin{array}{l}\left( {SAC} \right) \cap \left( {SBD} \right) = SO\\\left( {SAC} \right):AC \bot SO = \left\{ O \right\}\\\left( {SBD} \right):BD \bot SO = \left\{ O \right\}\end{array} \right\} \Rightarrow \left( {\left( {SAC} \right),\left( {SBD} \right)} \right) = \left( {AC,BD} \right) = \widehat {AOB}\)
+) Nếu \(\left( {SAC} \right) \bot \left( {SBD} \right) \Rightarrow \widehat {AOB} = {90^0} \Rightarrow AC \bot BD\)
Mà ABCD là hình chữ nhật nên ABCD là hình vuông.
+) Nếu ABCD là hình vuông \( \Rightarrow AC \bot BD \Rightarrow \widehat {AOB} = {90^0}\)
\( \Rightarrow \left( {\left( {SAC} \right),\left( {SBD} \right)} \right) = {90^0} \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right)\)
