Hoạt động 2
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ {0;2\pi } \right)\)
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.
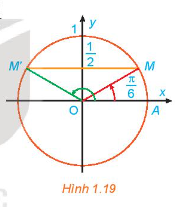

Nghiệm của phương trình \(\sin x = \frac{1}{2}\) là hoành độ các giao điểm của đường thẳng \(y = \frac{1}{2}\) và đồ thị hàm số \(y = \sin x\)

a) Từ Hình 1.19, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, - \frac{{5\pi }}{6}\)
b) Vì hàm số \(\sin x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
Luyện tập 2
Advertisements (Quảng cáo)
Giải các phương trình sau: a) \(\sin x = \frac{{\sqrt 2 }}{2}\); b) \(\sin 3x = - \sin 5x\)

Dựa vào công thức nghiệm tổng quát:
\(\sin x = m\; \Leftrightarrow \sin x = \sin \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}\left( {k \in \mathbb{Z}} \right)} \right.\)
Áp dụng công thức cộng lượng giác

a) \(\sin x = \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \sin x = \sin \frac{\pi }{4}\;\;\;\; \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)
b)
\(\begin{array}{l}\sin 3x = - \sin 5x\;\;\;\\\; \Leftrightarrow \,\,\,\sin 3x + \sin 5x = 0\;\;\;\;\;\;\\ \Leftrightarrow \,\,\,2\sin 4x\cos x = 0\;\end{array}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = 0}\\{\cos x = 0}\end{array}\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = \sin 0}\\{\cos x = \cos \frac{\pi }{2}}\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = k\pi }\\{x = \frac{\pi }{2} + k\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.} \right.\)
