Hoạt động 3
Cho điểm O và đường thẳng \(\Delta \) không đi qua O. Gọi d là đường thẳng đi qua O và song song với \(\Delta \). Xét hai mặt phẳng phân biệt tuỳ ý (P) và (Q) cùng chứa d. Trong các mặt phẳng (P), (Q) tương ứng kẻ các đường thẳng a, b cùng đi qua O và vuông góc với d (H.7.16). Giải thích vì sao mp(a, b) đi qua O và vuông góc với \(\Delta \).
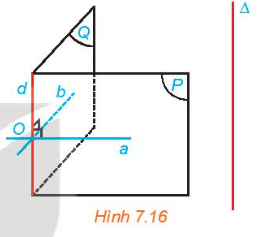

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

\(\left. \begin{array}{l}a \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot a\)
\(\left. \begin{array}{l}b \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot b\)
Mà \(a \cap b = \left\{ O \right\}\) \( \Rightarrow \) mp(a, b) đi qua O và vuông góc với \(\Delta \).
Hoạt động 4
Cho mặt phẳng (P) và điểm O. Trong mặt phẳng (P), lấy hai đường thẳng cắt nhau a, b tuỳ ý. Gọi \(\left( \alpha \right),\left( \beta \right)\) là các mặt phẳng qua O và tương ứng vuông góc với a, b (H.7.19).
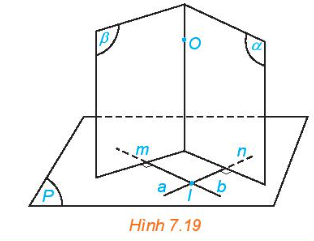
a) Giải thích vì sao hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) cắt nhau theo một đường thẳng \(\Delta \) đi qua O.
b) Nêu nhận xét về mối quan hệ giữa \(\Delta \) và (P).

Advertisements (Quảng cáo)
- 2 mặt phẳng cắt nhau theo 1 giao tuyến là đường thẳng.
- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

a) Vì \(\left( \alpha \right),\left( \beta \right)\) là các mặt phẳng qua O và giao 2 mặt phẳng là 1 đường thẳng nên hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) cắt nhau theo một đường thẳng đi qua O.
b) Gọi \(\Delta \) là giao tuyến của 2 \(\left( \alpha \right),\left( \beta \right)\)
\(\left. \begin{array}{l}a \bot \left( \alpha \right)\\\Delta \subset \left( \alpha \right)\end{array} \right\} \Rightarrow a \bot \Delta \)
\(\left. \begin{array}{l}b \bot \left( \beta \right)\\\Delta \subset \left( \beta \right)\end{array} \right\} \Rightarrow b \bot \Delta \)
Mà \(a \cap b = \left\{ I \right\} \Rightarrow \Delta \bot \left( P \right)\)
Luyện tập 2
Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.

Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng.

Vì AB và AC cùng vuông góc với một mặt phẳng (P) nên AB trùng AC
\( \Rightarrow \) A, B, C thẳng hàng.
