Hoạt động 4
Trong mặt phẳng tọa độ vẽ đường tròn tâm O bán kính R = 1. Chọn điểm gốc của đường tròn là giao điểm của đường tròn với trục . Ta quy ước chiều dương của đường tròn là chiều ngược chiều quay của kim đồng hồ và chiều âm là chiều quay của kim đồng hồ.
a) Xác định điểm trên đường tròn sao cho sđ\((OA,OM) = \frac{{5\pi }}{4}\)
b) Xác định điểm trên đường tròn sao cho sđ\((OA,ON) = - \frac{{7\pi }}{4}\)


Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là điểm M trên đường tròn lượng giác sao cho sđ\((OA,OM) = \alpha \)

a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng \(\frac{{5\pi }}{4}\) được xác định trong hình.
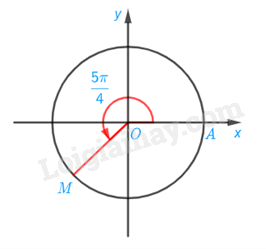
b) Điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng\( - \frac{{7\pi }}{4}\)được xác định là điểm chính giữa cung BA.
Luyện tập 4
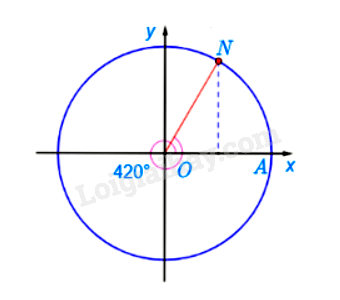
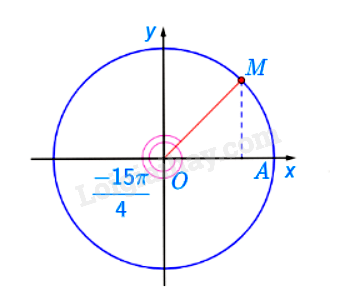
Xác định điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4}\)và \({420^ \circ }\)

Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là điểm M trên đường tròn lượng giác sao cho sđ\((OA,OM) = \alpha \)

Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)

Hoạt động 5
Nhắc lại khái niệm các giá trị lượng giác \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) của góc \(\alpha \)\(({0^ \circ } \le \alpha \le {180^ \circ })\) đã học ở lớp 10

Dựa vào kiến thức đã học để nhắc lại.

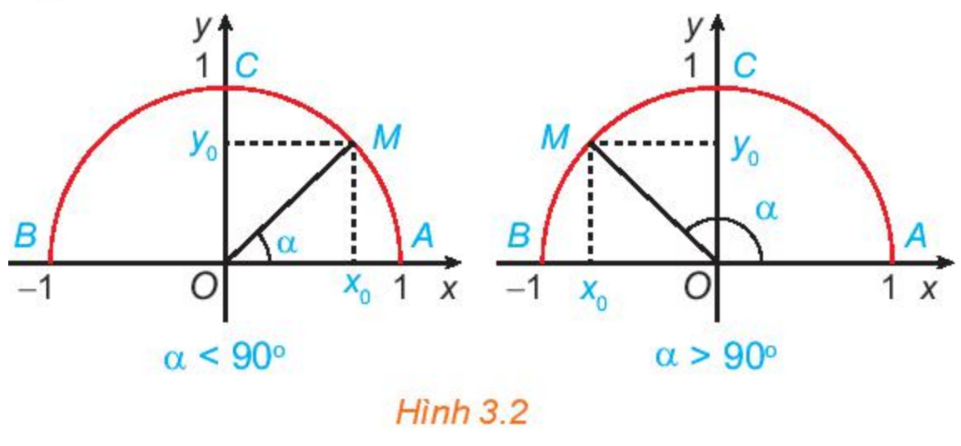
+) Nửa đường tròn đơn vị: nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (H.3.2).
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\)có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị nói trên để \(\widehat {xOM} = \alpha .\) Khi đó:
Advertisements (Quảng cáo)
\(\sin \alpha = {y_0}\) là tung độ của M
\(\cos \alpha = {x_0}\) là hoành độ của M
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\)
Luyện tập 5
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.

Áp dụng \(\sin \alpha = y\) ; \(\cos \alpha = x\) ; \(\tan \alpha =\frac{y}{x}\) ; \(\cot \alpha =\frac{x}{y}\)

a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
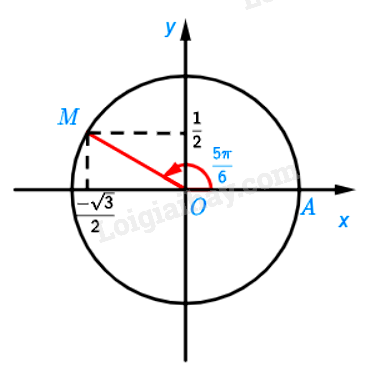
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)
Luyện tập 6
Sử dụng máy tính cầm tay để:
a) Tính: \(\cos \frac{{3\pi }}{7};\tan ( - {37^ \circ }25′)\)
b) Đổi \({179^ \circ }23’30”\) sang rađian;
c) Đổi \(\frac{{7\pi }}{9}\)(rad) sang độ.

Sử dụng máy tính cầm tay

a) \(\cos \frac{{3\pi }}{7} = 0,22252\);
\(\tan ( - {37^ \circ }25′) = -0,765018\)
b) Đổi 179°23’30” sang rađian ta thực hiện bấm phím lần lượt như sau:

Màn hình hiện 3,130975234
Vậy 179°23’30” ≈ 3,130975234 (rad).
c) \(\frac{{7\pi }}{9}\) (rad) = \(140^ \circ \)”.
