Hoạt động3
Cho đồ thị của hàm số \(y = {2^x}\) và \(y = 4\) như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình \({2^x} > 4.\)
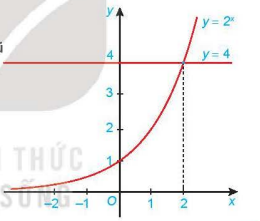

Quan sát đồ thị

Khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 là \(\left( {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({2^x} > 4\) là \(\left( {2; + \infty } \right)\)
Luyện tập3
Giải các bất phương trình sau:
Advertisements (Quảng cáo)
a) \(0,{1^{2x - 1}} \le 0,{1^{2 - x}};\)
b) \({3.2^{x + 1}} \le 1.\)

Xét bất phương trình dạng \({a^x} > b\)
+) a > 1, nghiệm của bất phương trình là \(x > {\log _a}b\)
+) 0 < a < 1, nghiệm của bất phương trình là \(x < {\log _a}b\)

a) \(0,{1^{2x - 1}} \le 0,{1^{2 - x}} \Leftrightarrow 2x - 1 \ge 2 - x \Leftrightarrow 3x \ge 3 \Leftrightarrow x \ge 1\)
b) \({3.2^{x + 1}} \le 1 \Leftrightarrow {2^{x + 1}} \le \frac{1}{3} \Leftrightarrow x + 1 \le {\log _2}\frac{1}{3} \Leftrightarrow x \le - {\log _2}3 - 1 = - {\log _2}3 - {\log _2}2 = - {\log _2}6\)
