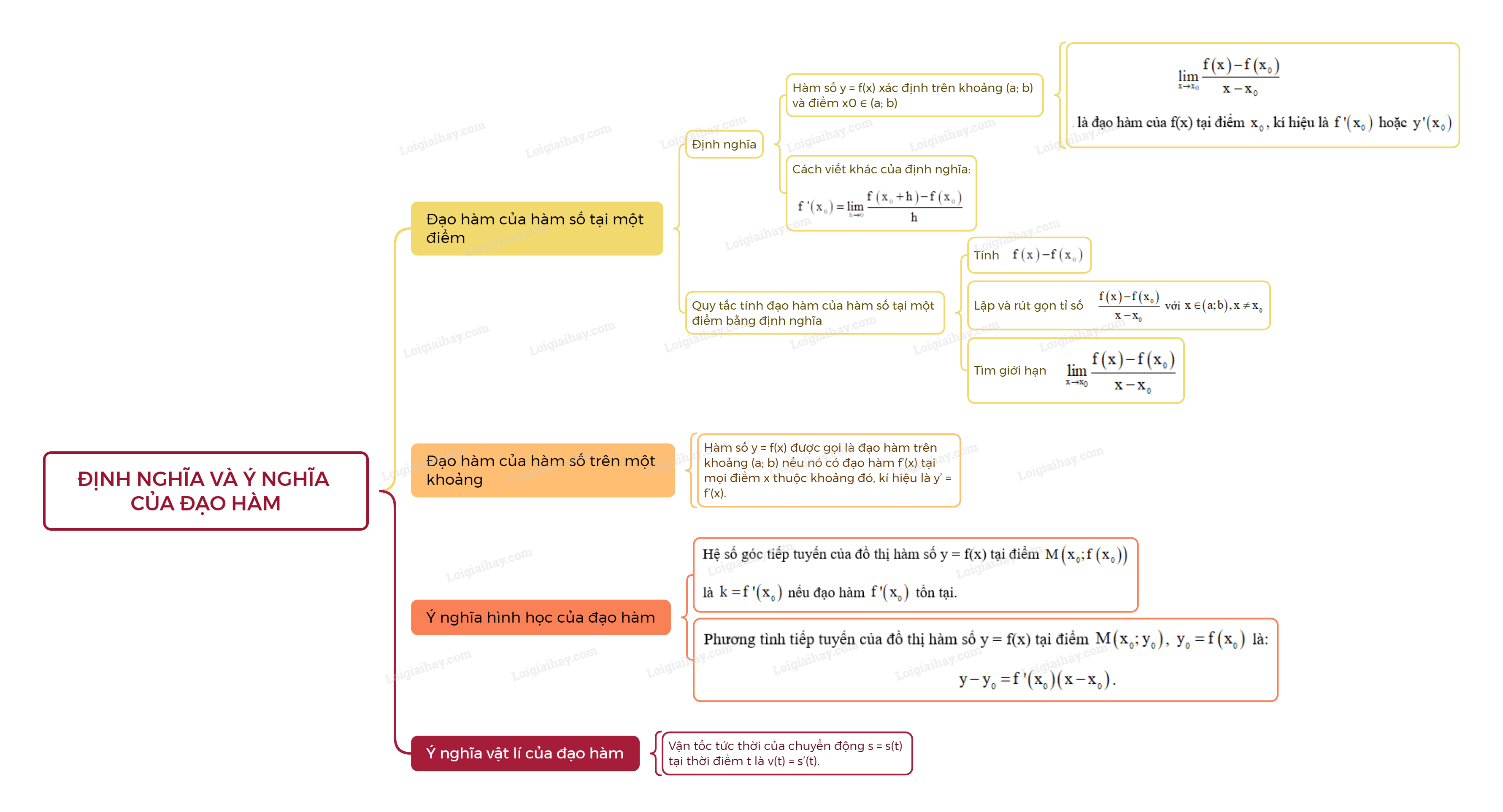
1. Đạo hàm của hàm số tại một điểm
- Định nghĩa:Cho hàm số y = f(x) xác định trên khoảng \(\left( {a;b} \right)\) và điểm \({x_0} \in \left( {a;b} \right)\). Nếu tồn tại giới hạn (hữu hạn)
\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\)
thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm \({x_0}\), kí hiệu là \(f’\left( {{x_0}} \right)\) hoặc \(y’\left( {{x_0}} \right)\).
- Cách viết khác của định nghĩa:
\(f’\left( {{x_0}} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {{x_0} + h} \right) - f\left( {{x_0}} \right)}}{h}\).
- Quy tắc tính đọa hàm của hàm số tại một điểm bằng định nghĩa:
Bước 1: Tính \(f\left( x \right) - f\left( {{x_0}} \right)\).
Bước 2: Lập và rút gọn tỉ số \(\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) với \(x \in \left( {a;b} \right),x \ne {x_0}\).
Bước 3: Tìm giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\).
Advertisements (Quảng cáo)
2. Đạo hàm của hàm số trên một khoảng
Hàm số y = f(x) được gọi là đạo hàm trên khoảng (a; b) nếu nó có đạo hàm f’(x) tại mọi điểm x thuộc khoảng đó, kí hiệu là y’ = f’(x).
3. Ý nghĩa hình học của đạo hàm
- Hệ số góc tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) là \(k = f’\left( {{x_0}} \right)\) nếu đạo hàm \(f’\left( {{x_0}} \right)\) tồn tại.
- Phương tình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(M\left( {{x_0};{y_0}} \right)\), \({y_0} = f\left( {{x_0}} \right)\) là:
\(y - {y_0} = f’\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
4. Ý nghĩa vật lý của đạo hàm
Vận tốc tức thời của chuyển động s = s(t) tại thời điểm t là v(t) = s’(t).