Bài 7 trang 114 sgk hình học 11: Bài 4. Hai mặt phẳng vuông góc. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c...
Bài 7. Cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có \(AB = a, BC = b, CC’ = c\).
a) Chứng minh rằng mặt phẳng \((ADC’B’)\) vuông góc với mặt phẳng \((ABB’A’)\).
b) Tính độ dài đường chéo \(AC’\) theo \(a, b, c\).

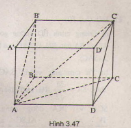
a) Ta có: \(DA ⊥ (ABB’A’), DA ⊂ (ADC’B’)\)
Advertisements (Quảng cáo)
\(\Rightarrow (ADC’B’) \bot(ABB’A’)\).
b) Xét tam giác vuông \(ACC’\))
\(AC’ = \sqrt {A{C^2} + CC{‘^2}} = \sqrt {A{D^2} + D{C^2} + CC{‘^2}}\)
\(=\sqrt{a^{2}+b^{2}+c^{2}}.\)
Ghi nhớ: Hai mặt phẳng vuông góc với nhau khi mặt này chứa một đường thẳng vuông góc với mặt kia.
