Bài 9 trang 114 sgk Hình học 11: Bài 4. Hai mặt phẳng vuông góc. Cho hình chóp tam giác đều S.ABC...
Bài 9. Cho hình chóp tam giác đều \(S.ABC \) có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\).

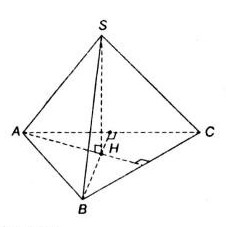
Chóp tam giác đều nên ta có \(H\) là trực tâm của tam giác \(ABC\)
Advertisements (Quảng cáo)
\(SH ⊥ (ABC) \Rightarrow SH ⊥ BC\) và \(AH ⊥ BC\) (vì \(H\) là trực tâm)
Suy ra \( BC ⊥ (SAH)\)
\(SA\subset (SAH)\Rightarrow BC ⊥ SA\).
Chứng minh tương tự, ta có \(SB ⊥ AC\).
