Cho tam giác AIB có IA = IB = 2a, \(\widehat {AIB}\) =1200. Trên đường thẳng \(\Delta \) vuông góc với mp(AIB) tại I, lấy các điểm C và D sao cho ABC là tam giác vuông, ABD là tam giác đều.
1) Tính thể tích và diện tích toàn phần cửa tứ diện ABCD.
2) Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD.
3) Tính bán kính mặt cầu nội tiếp tứ diện ABCD.

Vì IA = IB = 2a, \(\widehat {AIB}\) =1200 nên \(A{B^2} = I{A^2} + I{B^2} - 2IA.IB.\cos \) \(\widehat {AIB}\) =12a2, từ đó \(AB = 2a\sqrt 3 \). Do \(CD \bot mp(AIB)\) tại I, IA = IB nên CA = CB. Kết hợp với giả thiết ABC là tam giác vuông, ta có ABC là tam giác vuông tại C và \(CA = CB = {{AB} \over {\sqrt 2 }} = a\sqrt 6 .\)
Vì ABD là tam giác đều nên \(AD = AB = 2a\sqrt 3 .\)
Từ đó \(C{I^2} = A{C^2} - A{I^2} = 6{a^2} - 4{a^2} = 2{a^2},\) tức là \(CI = a\sqrt 2 ,\)
\(D{I^2} = A{D^2} - A{I^2} = 12{a^2} - 4{a^2} = 8{a^2},\) tức là \(DI =2 a\sqrt 2 ,\)
\( \bullet \) Hai điểm C, D thuộc đường thẳng \(\Delta \) vuông góc với mp(AIB) tại điểm I nên có hai trường hợp xảy ra.
+) Trường hợp 1. C, D nằm về hai phía đối với điểm I (h.91a).
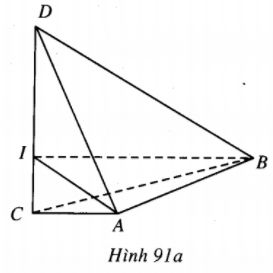
Dễ thấy \(CD = 3a\sqrt 2 \), từ đó \(C{D^2} = 18{a^2}\); mặt khác \(A{C^2} + A{D^2} = 18{a^2},\) tức là \(C{D^2} = A{C^2} + A{D^2}.\) Như vậy \(\widehat {CAD}\) = 900. Tương tự ta cũng có \(\widehat {CBD}\) = 900.
1) \({V_{ABCD}} = {V_{D.AIB}} + {V_{C.AIB}}\)
\(= {1 \over 3}.{1 \over 2}AI.BI\sin \widehat {AIB}.(ID+IC)\)
\( = {1 \over 3}.{1 \over 2}.2a.2a.{{\sqrt 3 } \over 2}.3a\sqrt 2 = {a^3}\sqrt 6 .\)
Gọi \({S_{tp}}\) là diện tích toàn phàn của tứ diện ABCD thì
Advertisements (Quảng cáo)
\(\eqalign{ {S_{tp}} &= {S_{ACD}} + {S_{BCD}} + {S_{ABC}} + {S_{ABD}} \cr & = 2.{1 \over 2}CD.AI + {{A{C^2}} \over 2} + {{A{B^2}\sqrt 3 } \over 4} \cr & = 3a\sqrt 2 .2a + {1 \over 2}.6{a^2} + 12{a^2}.{{\sqrt 3 } \over 4} \cr & = 6{a^2}\sqrt 2 + 3{a^2} + 3{a^2}\sqrt 3 \cr & = 3{a^2}(1 + \sqrt 3 + 2\sqrt 2 ) \cr} \)
2) Vì \(\widehat {CAD} = \widehat {CBD}\) = 900 nên CD là đường kính của mặt cầu ngoại tiếp tứ diện ABCD, từ đó bán kính mặt cầu phải tìm bằng \({{3a\sqrt 2 } \over 2}\) và diện tích mặt cầu bằng \(18\pi {a^2}.\)
3) Gọi r là bán kính mặt cầu nội tiếp tứ diện ABCD thì dễ thấy \(r = {{3{V_{ABCD}}} \over {{S_{tp}}}},\) từ đó
\(\eqalign{ r = &{{3{a^3}\sqrt 6 } \over {3{a^2}(1 + \sqrt 3 + 2\sqrt 2 )}} \cr & = {{a\sqrt 6 } \over {1 + \sqrt 3 + 2\sqrt 2 }}. \cr} \)
+) Trường hợp 2. C, D nằm về một phía đổi với điểm I (h.91b)
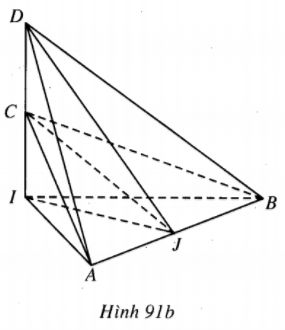
1)
\(\eqalign{ & {V_{ABCD}} = {V_{DAIB}} - {V_{CAIB}} = {{{a^3}\sqrt 6 } \over 3}, \cr & {S_{tp}} = 2{a^2}\sqrt 2 + 3{a^2} + 3{a^2}\sqrt 3 \cr & \;\;\;\;\;\;= {a^2}(3 + 2\sqrt 2 + 3\sqrt 3 ). \cr} \)
2) Gọi J là trung điểm của AB thì JA = JB = JC.
Xét đường thẳng \({\Delta _1}\) đi qua J và vuông góc với mp(ABC). Khi đó, mọi điểm thuộc \({\Delta _1}\) cách đều các điểm A, B, C và \({\Delta _1}\) nằm trong mp(CDJ) ( do mp(CDJ) vuông góc với mp(ABC)). Trong mp(CDJ), đường trung trực của CD cắt \({\Delta _1}\) tại điểm O thì OA = OB = OC = OD = R (h.91c).

Ta có \({\rm{IJ}} = a,CJ = a\sqrt 3 .\) Kẻ \(OH \bot IJ\) thì
\(OH = IK = {{3a\sqrt 2 } \over 2}.\) Xét các tam giác ICJ và HJO, ta có sin C = sin J hay \({{{\rm{IJ}}} \over {JC}} = {{OH} \over {JO}}.\) Vậy \(JO = {{OH.JC} \over {{\rm{IJ}}}} = {{{{3a\sqrt 2 } \over 2}.a\sqrt 3 } \over a} = {{3a\sqrt 6 } \over 2}.\)
Từ đó \(O{C^2} = C{J^2} + J{O^2} = 3{a^2} + {{54{a^2}} \over 4} = {{66{a^2}} \over 4}.\)
Vậy diện tích mặt cầu phải tìm là \(66\pi {a^2}.\)
3) \(r = {{{a^3}\sqrt 6 } \over {{a^2}\left( {3 + 2\sqrt 2 + 3\sqrt 3 } \right)}} = {{a\sqrt 6 } \over {3 + 3\sqrt 3 + 2\sqrt 2 }}.\)
