Xét hình chóp tứ giác đều S.ABCD có cạnh đáy và chiều cao thay đổi. Tìm hệ thức liên hệ giữa cạnh đáy và chiều cao của hình chóp để \({{{V_1}} \over {{V_2}}}\) đạt giá trị nhỏ nhất, ở đó \({V_1},{V_2}\) lần lượt là thể tích của các hình cầu ngoại tiếp và nội tiếp hình chóp.

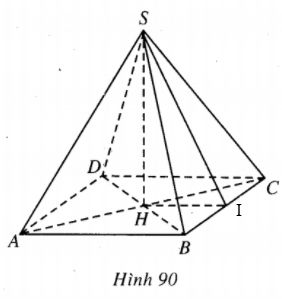
Gọi x là độ dài cạnh đáy, y là chiều cao của hình chóp; R, r lần lượt là bán kính mặt cầu ngoại tiếp và nội tiếp hình chóp thì dễ tính được \(R = {{{x^2} + 2{y^2}} \over {4y}},\)
\(r = {{xy} \over {x + \sqrt {{x^2} + 4{y^2}} }}\). Vậy
\({{{V_1}} \over {{V_2}}} = {\left( {{R \over r}} \right)^3} = {\left[ {{{({x^2} + 2{y^2})(x + \sqrt {{x^2} + 4{y^2}} )} \over {4x{y^2}}}} \right]^3}.\)
Từ đó \({{{V_1}} \over {{V_2}}}\) nhỏ nhất khi và chỉ khi \({R \over r}\) nhỏ nhất.
Gọi \(\varphi \) là góc giữa mặt bên và mặt đáy của hình chóp thì \(\varphi = \widehat {SIH}\) (I là trung điểm của BC ). Khi đó \(y = {x \over 2}\tan \varphi \Rightarrow 4{y^2} = {x^2}{\tan ^2}\varphi ,\) từ đó
\(\eqalign{
& {R \over r} = {{\left( {{x^2} + {{{x^2}{{\tan }^2}\varphi } \over 2}} \right)\left( {x + \sqrt {{x^2} + {x^2}{{\tan }^2}\varphi } } \right)} \over {{x^3}{{\tan }^2}\varphi }} \cr
& = {{\left( {2 + {{\tan }^2}\varphi } \right)\left( {1 + {1 \over {\cos \varphi }}} \right)} \over {2{{\tan }^2}\varphi }} \cr
& = {{\left( {1 + {1 \over {{{\cos }^2}\varphi }}} \right)\left( {{{\cos \varphi + 1} \over {\cos \varphi }}} \right)} \over {2 \cdot {{1 - {{\cos }^2}\varphi } \over {{{\cos }^2}\varphi }}}} \cr
& = {{1 + {{\cos }^2}\varphi } \over {2\cos \varphi \left( {1 - \cos \varphi } \right)}} = {1 \over 2} \cdot {{1 + {t^2}} \over {t\left( {1 - t} \right)}} \cr} \)
(với \(0 < t = \cos \varphi < 1.\))
Advertisements (Quảng cáo)
Như vậy, \({{{V_1}} \over {{V_2}}}\) nhỏ nhất khi và chỉ khi \(f(t) = {{1 + {t^2}} \over {t(1 - t)}}\) đạt giá trị nhỏ nhất (0< t < 1).
Ta có :
\(\eqalign{ & f'(t) = {{2t(1 - {t^2}) - (1 - 2t)(1 + {t^2})} \over {{{\left[ {t(1 - t)} \right]}^2}}} \cr & = {{2{t^2} - 2{t^3} - 1 + 2t - {t^2} + 2{t^3}} \over {{{\left[ {t(1 - t)} \right]}^2}}} = {{{t^2} + 2t - 1} \over {{t^2}{{(1 - t)}^2}}}. \cr & \cr} \)
\(f'(t) = 0 \Leftrightarrow {t^2} + 2t - 1 = 0 \Leftrightarrow t = - 1 + \sqrt 2 \) (do 0< t <1).
Ta có bảng biến thiên
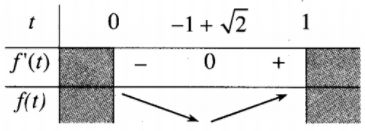
Vậy f(t) đạt giá trị nhỏ nhất tại \(t = - 1 + \sqrt 2 \), tức là \(\cos \varphi = -1 + \sqrt 2 \)
\(\eqalign{ & \Leftrightarrow 1 + {\tan ^2}\varphi = {1 \over {3 - 2\sqrt 2 }} \cr & \Leftrightarrow {\tan ^2}\varphi = {{1 - 3 + 2\sqrt 2 } \over {3 - 2\sqrt 2 }} = {{2\left( {\sqrt 2 - 1} \right)} \over {{{\left( {\sqrt 2 - 1} \right)}^2}}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {2 \over {\sqrt 2 - 1}} = 2\left( {\sqrt 2 + 1} \right) \cr & \Rightarrow \tan \varphi = \sqrt {2\sqrt 2 + 2} . \cr} \)
Vậy hệ thức liên hệ giữa x và y là \(y = x{{\sqrt {2\sqrt 2 + 2} } \over 2}.\)
Khi đó \({{{V_1}} \over {{V_2}}}\) đạt giá trị nhỏ nhất.
