Gọi r và h lần lượt là bán kính đáy và chiều cao của một hình nón. Kí hiệu \({V_1},{V_2}\) lần lượt là thể tích hình nón và thể tích hình cầu nội tiếp hình nón.
1) Tỉ số \({{{V_1}} \over {{V_2}}}\) theo r, h.
2) Khi r và h thay đổi, tìm giá trị bé nhất của tỉ số \({{{V_1}} \over {{V_2}}}\).

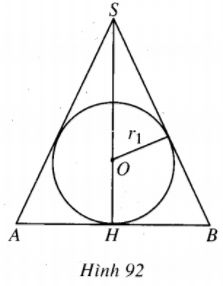
Gọi (P) là mặt phẳng đi qua trục của hình nón thì (P) cắt hình nón theo tam giác cân SAB, cắt mặt cầu theo đường tròn lớn, đường tròn này nội tiếp tam giác cân. Khi đó, bán kính \({r_1}\) của hình cầu nội tiếp hình nón được tính bởi công thức
\({r_1} = {{rh} \over {r + \sqrt {{h^2} + {r^2}} }}.\)
1) Thể tích hình nón là \({V_1} = {1 \over 3}\pi {r^2}h.\)
Thể tích hình cầu nội tiếp hình nón là \({V_2} = {{4\pi } \over 3}{\left( {{{rh} \over {r + \sqrt {{r^2} + {h^2}} }}} \right)^3}.\)
Vậy \({{{V_1}} \over {{V_2}}} = {1 \over 4}{{{{\left( {r + \sqrt {{r^2} + {h^2}} } \right)}^3}} \over {r{h^2}}}.\)
Advertisements (Quảng cáo)
2) \({{{V_1}} \over {{V_2}}} = {1 \over 4}{{{{\left( {\sqrt {1 + {{{h^2}} \over {{r^2}}}} + 1} \right)}^3}} \over {{{{h^2}} \over {{r^2}}}}} = {1 \over 4}{{{{\left( {1 + \sqrt {1 + x} } \right)}^3}} \over x},\) ở đó \({{{h^2}} \over {{r^2}}} = x > 0.\)
Xét \(f(x) = {{{{\left( {1 + \sqrt {1 + x} } \right)}^3}} \over {4x}},f'(x) = {{{{\left( {\sqrt {1 + x} + 1} \right)}^2}\left( {x - 2 - 2\sqrt {1 + x} } \right)} \over {4.2{x^2}\sqrt {x + 1} }}.\)
Vì \({{{{\left( {\sqrt {1 + x} + 1} \right)}^2}} \over {4.2{x^2}\sqrt {x + 1} }} > 0\) nên khi xét dấu của f(x), ta chỉ cần xét dấu của \(g(x) = x - 2 - 2\sqrt {1 + x} .\) Ta có \(g'(x) = 1 - {1 \over {\sqrt {x + 1} }}.\)
Dễ thấy g’(x) > 0 vì khi x > 0 thì \({1 \over {\sqrt {x + 1} }} < 1,\) đồng thời g(x) = 0\( \Leftrightarrow x = 8.\)
Vậy g(x) là hàm tăng trên miền x > 0 và g(8) = 0 nên
với \(0 < x \le 8\) thì \(g(x) \le 0;\)
với \(8 < x < + \infty \) thì g(x) > 0.
Bảng biến thiên của f(x)

Vậy giá trị bé nhất của \({{{V_1}} \over {{V_2}}}\) bằng 2.
