a) Chứng minh rằng nếu ba số phức \({z_1},{z_2},{z_3}\) thỏa mãn
\(\left\{ \matrix{\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1 \hfill \cr{z_1} + {z_2} + {z_3} = 1 \hfill \cr} \right.\)
Thì một trong ba số đó phải bằng 1.
b) Giải hệ phương trình ba ẩn phức \({z_1},{z_2},{z_3}\) sau:
\(\left\{ \matrix{ \left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1 \hfill \cr{z_1}{z_2} + {z_3} = 1 \hfill \cr{z_1}{z_2}{z_3} = 1 \hfill \cr} \right.\)
Giải
Advertisements (Quảng cáo)
a) Viết \(1 - {z_1} = {z_2} + {z_3}\)
Nếu \({z_1} = 1\) thì \({z_2} + {z_3} = 0\)
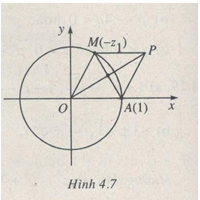
Nếu \({z_1} \ne 1\) thì \(1 - {z_1} \ne 0\), điểm P biểu diễn số \(1 + \left( { - {z_1}} \right) = {z_2} + {z_3}\) không trùng với O nên do \(1 = \left| { - {z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right|\), đường trung trực OP cắt đường tròn đơn vị tại hai điểm biểu diễn \(1, - {z_1}\) và cũng là hai điểm biểu diễn \({z_2},{z_3}\) (h.4.7). Vậy \({z_2} = 1,{z_3} = - {z_1}\) hoặc \({z_2} = - {z_1},{z_3} = 1\). Tóm lại hoặc \({z_1} = 1\) hoặc \({z_2} = 1\) hoặc \({z_3} = 1\) và tổng hai số z còn lại bằng 0
b) Từ hai phương trình đầu của hệ, theo câu a) có thể coi \({z_1} = 1,{z_2} + {z_3} = 0\). Khi đó điều kiện \(z_1z_2z_3=1\) kéo theo hoặc \({z_2} = i,{z_3} = - i\) hoặc \({z_2} = - i,{z_3} = i.\). Suy ra hệ có 6 nghiệm do đổi chỗ các phần tử của bộ ba \(\left( {1,i, - i} \right)\)