Cho hàm số: y = 4x3 + mx (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.
b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.
Hướng dẫn làm bài:
a) \(y = 4{x^3} + x,y’ = 12{x^2} + 1 > 0,\forall x \in R\)
Bảng biến thiên:
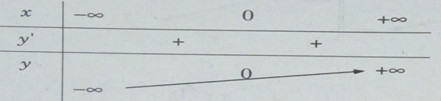
Đồ thị:
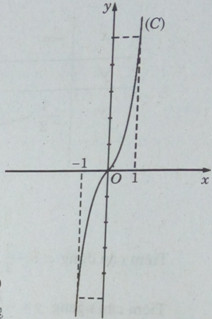
b) Giả sử tiếp điểm cần tìm có tọa độ (x0; y0) thì \(f'({x_0}) = 12x_0^2 + 1 = 13\) (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: \({x_0} = \pm 1\)
Advertisements (Quảng cáo)
Vậy có hai tiếp tuyến phải tìm là \(y = 13x \pm 8\)
c) Vì y’ = 12x2 + m nên : \(m \ge 0:y” = - 6({m^2} + 5m)x + 12m\)
+) Với \(m \ge 0\) ta có y’ > 0 (khi m = 0 ; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi \(m \ge 0:y” = - 6({m^2} + 5m)x + 12m\)
+) Với m < 0 thì \(y{\rm{ }} = {\rm{ }}0 \Leftrightarrow x = \pm \sqrt {{{ - m} \over {12}}} \)
Từ đó suy ra:
y’ > 0 với \( - \infty < x < - \sqrt {{{ - m} \over {12}}} \) và \(\sqrt {{{ - m} \over {12}}} < x < + \infty \)
y’ < 0 với \( - \sqrt {{{ - m} \over {12}}} < x < \sqrt {{{ - m} \over {12}}} \)
Vậy hàm số (1) đồng biến trên các khoảng \(( - \infty ; - \sqrt {{{ - m} \over {12}}} ),(\sqrt {{{ - m} \over {12}}} ; + \infty )\) và nghịch biến trên khoảng \(( - \sqrt {{{ - m} \over {12}}} ;\sqrt {{{ - m} \over {12}}} )\)
