Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn dây thứ nhất được uốn thành hình vuông, đoạn dây thứ hai được uốn thành hình tròn (h.1.7).
Phải cắt sợi dây như thế nào để tổng diện tích của hinh vuông và hinh tròn là nhỏ nhất ?
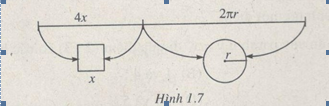
Giải
Gọi x là đọ dài cạnh hình vuông và r là bán kính hình tròn.
Độ dài cạnh hình vuông \(x = {{60} \over {\pi + 4}}\) (cm)
Đoạn dây được uốn thành hình vuông có cạnh có độ dài là \({{240} \over {\pi + 4}} \approx 33,6\) (cm)
Bán kính đường tròn \(r = {{30} \over {\pi + 4}}\) (cm)
Advertisements (Quảng cáo)
Đoạn dây được uốn thành vòng tròn có độ dài là \({{60\pi } \over {\pi + 4}} \approx 26,4\) (cm)
Ta có
\(4x + 2\pi r = 60\)
Từ \(x = {1 \over 2}\left( {30 - \pi r} \right),0 < r < {{30} \over \pi }\)
Tổng diện tích hình vuông và hình tròn là
\(S = \pi {r^2} + {x^2} = \pi {r^2} + {1 \over 4}{\left( {30 - \pi r} \right)^2}\)
Dễ thấy S đạt giá trị nhỏ nhất tại điểm \(r = {{30} \over {\pi + 4}}\)
