Chứng minh rằng trong các hình hộp chữ nhật có đáy là một hình vuông và thể tích là 1000, hình lập phương có diện tích toàn phần là nhỏ nhất.
Giải
Câu 1.78 trang 26 sách bài tập Giải tích 12 Nâng cao
Một hình chóp với tứ giác đều ngoài tiếp hình cầu bán kính a.
a) Chứng mình rằng thể tích của hình chóp là
\(V = {{4{a^2}{x^2}} \over {3(x - 2a)}}.\)
Trong đó x là chiều cao của hình chóp.
b) Với giá trị nào của x,hình chóp có thể tích là nhỏ nhất ?
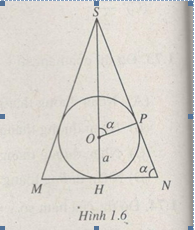
Hướng dẫn a) Mặt phẳng đi qua đường cao SH của hình chóp và trung điểm M của một cạnh đáy cắt hình chóp theo tam giác cân SMN và cắt hình cầu theo tâm O bán kính a nội tiếp tam giác SMN (h.1.6).
Có thể tính thể tích hình chóp theo x và \(\alpha = \widehat {SNH}\). Sau đó sử dụng đẳng thức \(x = a + {\rm{OS}}\) để tìm hệ thức giữa a, x và \(\alpha \)
Advertisements (Quảng cáo)
Giải
b) x = 4a.
Hướng dẫn. a) ta có \(HN = x\cot \alpha ;MN = 2x\cot \alpha \) . Thể tích hình chóp là
\(V = {1 \over 3}M{N^2}.SH = {4 \over 3}{x^3}{\cot ^2}\alpha \)
Ta tính \({\cot ^2}\alpha \) theo a và x. Từ đẳng thức SH = OH + OS ta có \(x = a + {a \over {{\rm{cos }}\alpha }}\); do đó \({\rm{cos }}\alpha = {a \over {x - a}}\)
\({\sin ^2}\alpha = 1 - c{\rm{o}}{{\rm{s}}^2}\alpha = 1 - {{{a^2}} \over {{{\left( {x - a} \right)}^2}}} = {{{x^2} - 2ax} \over {{{\left( {x - a} \right)}^2}}}\)
\({\cot ^2}\alpha = {{c{\rm{o}}{{\rm{s}}^2}\alpha } \over {{{\sin }^2}\alpha }} = {{{a^2}} \over {x{{\left( {x - 2a} \right)}^2}}}\)
Từ đó suy ra công thức cần chứng minh.
b) Chú ý rằng V xác định với x > 2a
