Cho hàm số: y = f(x) = x4 – 2mx2 + m3 – m2
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1.
b) Xác định m để đồ thị (Cm) của hàm số đã cho tiếp xúc với trục hoành tại hai điểm phân biệt.
Hướng dẫn làm bài:
a)
\(\eqalign{
& y = {x^4} - 2{x^2} \cr
& y’ = 4{x^3} - 4x = 4x({x^2} - 1) \cr
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \cr} \)
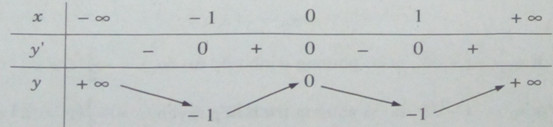
Bảng biến thiên:
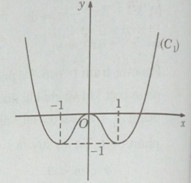
Đồ thị
Advertisements (Quảng cáo)
b) \(y’ = 4{x^3} - 4mx = 4x({x^2} - m)\)
Để (Cm) tiếp xúc với trục hoành tại hai điểm phân biệt thì điều kiện cần và đủ là phương trình y’ = 0 có hai nghiệm phân biệt khác 0 và yCT = 0.
+) Nếu \(m \le 0\) thì \({x^2} - m \ge 0\) với mọi x nên đồ thị không thể tiếp xúc với trục Ox tại hai điểm phân biệt.
+) Nếu m > 0 thì y’ = 0 khi \(x = 0;x = \pm \sqrt m \) .
\(\eqalign{
& f(\sqrt m ) = 0 \Leftrightarrow {m^2} - 2{m^2} + {m^3} - {m^2} = 0 \cr
& \Leftrightarrow {m^2}(m - 2) = 0 \Leftrightarrow m = 2 \cr} \)
(do m > 0)
Vậy m = 2 là giá trị cần tìm.
