Giải các phương trình sau bằng phương pháp đồ thị:
a) \({2^{ - x}} = 3x + 10\)
b) \({(\frac{1}{3})^{ - x}} = - 2x + 5\)
c) \({(\frac{1}{3})^x} = x + 1\)
d) \({3^x} = 11 - x\)
Hướng dẫn làm bài:
a) Vẽ đồ thị của hàm số: \(y = {2^{ - x}}\) và đường thẳng y = 3x +10 trên cùng một hệ trục tọa độ (H. 57) ta thấy chúng cắt nhau tại điểm có hoành độ x = -2. Thử lại, ta thấy x = -2 thỏa mãn phương trình đã cho.
Mặt khác, hàm số \(y = {2^{ - x}} = {(\frac{1}{2})^x}\) luôn nghịch biến, hàm số y = 3x + 10 luôn đồng biến.
Vậy x = -2 là nghiệm duy nhất.
Advertisements (Quảng cáo)
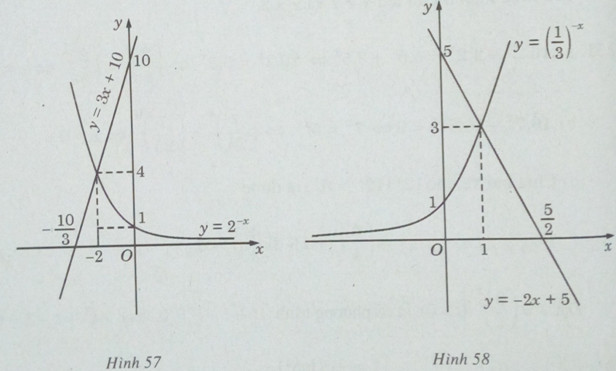
b) Vẽ đồ thị của hàm số \(y = {(\frac{1}{3})^{ - x}}\) và đường thẳng y = -2x + 5 trên cùng một hệ trục tọa độ (H.58), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Thử lại, ta thấy x = 1 thỏa mãn phương trình đã cho.
Mặt khác, hàm số \(y = {(\frac{1}{3})^{ - x}} = {3^x}\) luôn đồng biến, hàm số y = -2x + 5 luôn nghịch biến.
Vậy x = 1 là nghiệm duy nhất.
c) Vẽ đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.59), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0. Thử lại, ta thấy x = 0 thỏa mãn phương trình đã cho. Mặt khác, \(y = {(\frac{1}{3})^x}\) là hàm số luôn nghịch biến, hàm số y = x +1 luôn đồng biến.
Vậy x = 0 là nghiệm duy nhất.
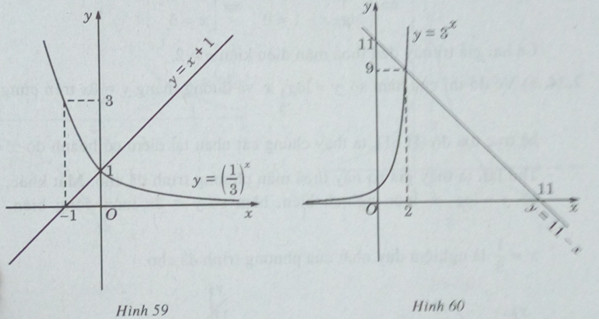
d) Vẽ đồ thị của hàm số và đường thẳng y = 11 – x trên cùng một hệ trục tọa độ (H.60), ta thấy chúng cắt nhau tại điểm có hoành độ x = 2. Thử lại, ta thấy x = 2 thỏa mãn phương trình đã cho. Mặt khác, \(y = {3^x}\) luôn đồng biến , y = 11 – x luôn nghịch biến . Vậy x = 2 là nghiệm duy nhất.
