Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) y = 2x – x2 , x + y = 2 ;
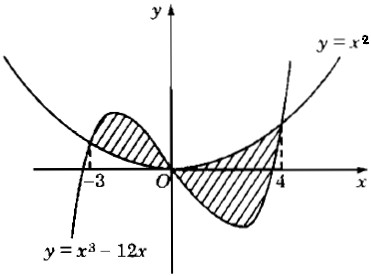
b) y = x3 – 12x , y = x2
c) x + y = 1 ; x + y = -1 ; x – y = 1 ; x – y = -1 ;
d) \(y = {1 \over {1 + {x^2}}},y = {1 \over 2}\)
e) y = x3 – 1 và tiếp tuyến với y = x3 – 1 tại điểm (-1; -2).
Hướng dẫn làm bài
a) \({1 \over 6}\)
Advertisements (Quảng cáo)
b) \(78{1 \over {12}}\) .HD: \(S = \int\limits_{ - 3}^0 {({x^3} - 12x - {x^2})dx + } \int\limits_0^4 {({x^2} - {x^3} + 12x)dx} \)
c) 2 ; HD: \(S = 4\int\limits_0^1 {(1 - x)dx} \)
d) \({\pi \over 2} - 1\)
HD: \(S = 2\int\limits_0^1 {({1 \over {1 + {x^2}}} - {1 \over 2})dx = 2\int\limits_0^1 {{1 \over {1 + {x^2}}}dx} - 1} \)
Đặt \(x = \tan t\) để tính \(\int\limits_0^1 {{1 \over {1 + {x^2}}}} dx\)
e) \({{27} \over 4}\) .HD: Phương trình tiếp tuyến tại (-1; -2) là y = 3x + 1. Do đó, diện tích :\(S = \int\limits_{ - 1}^2 {(3x + 1 - {x^3} + 1)dx = \int\limits_{ - 1}^2 {(3x + 2 - {x^3})dx} } \)
