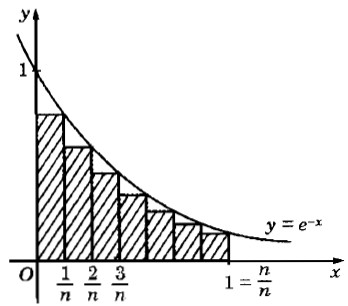
Một hình phẳng được giới hạn bởi \(y = {e^{ - x}},y = 0,x = 0,x = 1\). Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
b) Tìm \(\mathop {\lim }\limits_{n \to \infty } {S_n}\) và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Hướng dẫn làm bài
Advertisements (Quảng cáo)
a) \({S_n} = {{{1 \over n}(1 - {e^{ - 1}})} \over {{e^{{1 \over n} - 1}}}}\) . HD: Theo hình 80 ta có:
\({S_n} = {1 \over n}{\rm{[}}{e^{ - {1 \over n}}} + {e^{ - 2{1 \over n}}} + ... + {e^{ - {n \over n}}}{\rm{]}} = {1 \over n}{e^{ - {1 \over n}}}{{1 - {e^{ - 1}}} \over {1 - {e^{ - {1 \over n}}}}} = {{{1 \over n}(1 - {e^{ - 1}})} \over {{e^{{1 \over n}}} - 1}}\)
b) \(\mathop {\lim }\limits_{n \to \infty } {S_n} = 1 - {e^{ - 1}}\)
Mặt khác \(\int\limits_0^1 {{e^{ - x}}dx = 1 - {e^{ - 1}}} \)
