Advertisements (Quảng cáo)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số \(y = {{4x + 4} \over {2x + 1}}\)
b) Từ (C) suy ra đồ thị của hàm số \(y = |{{4x + 4} \over {2x + 1}}|\)
c) Viết phương trình tiếp tuyến với (C) , biết rằng tiếp tuyến đó song song với đường thẳng \(y = – {1 \over 4}x – 3\)
Hướng dẫn làm bài:
a) \(y = {{4x + 4} \over {2x + 1}}\)
Tập xác định: \(D = R\backslash {\rm{\{ }} – {1 \over 2}{\rm{\} }}\)
Ta có \(y’ = – {4 \over {{{(2x + 1)}^2}}}\)
Bảng biến thiên:
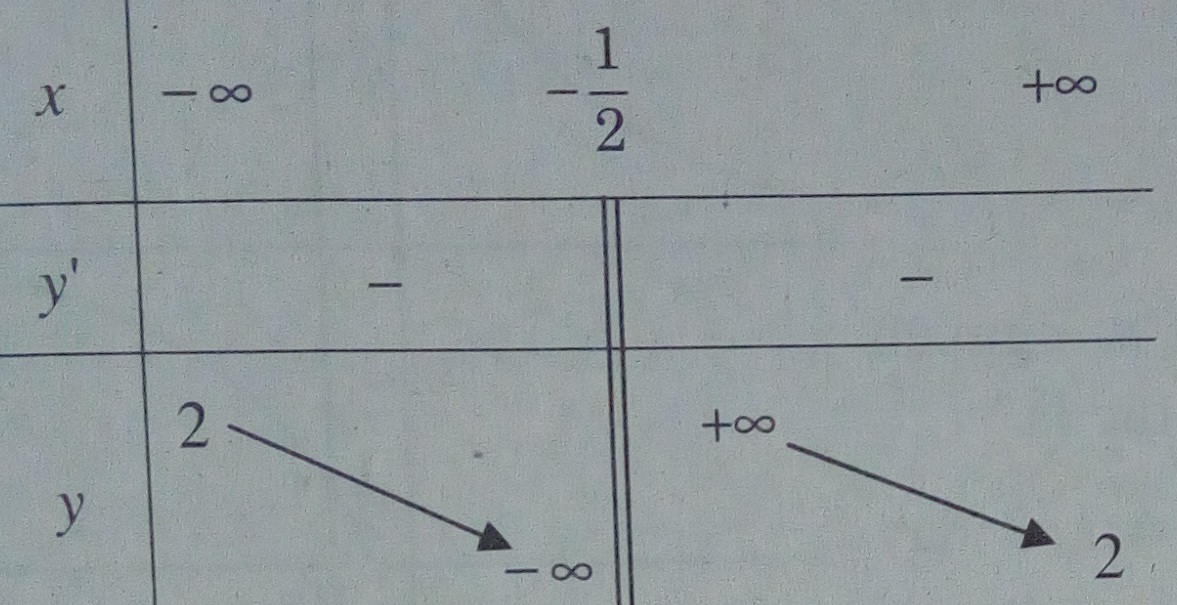
Hàm số nghịch biến trên các khoảng \(( – \infty ; – {1 \over 2})\) và \(( – {1 \over 2}; + \infty )\)
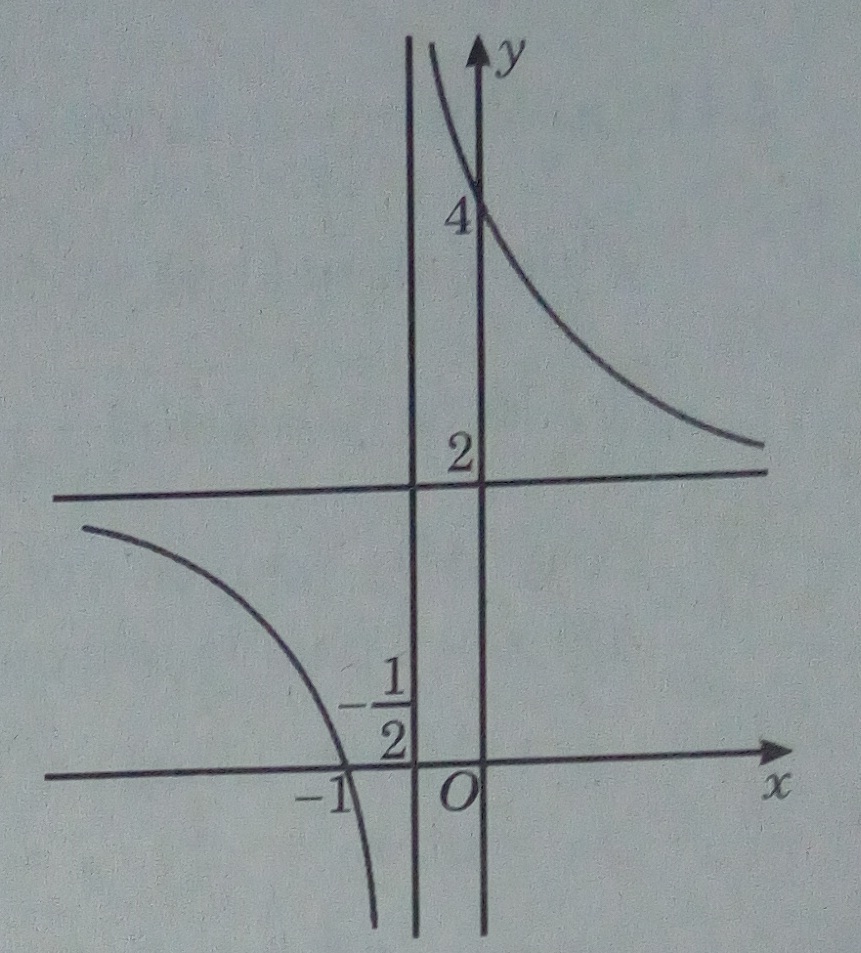
Tiệm cận đứng: \(x = – {1 \over 2}\) ; Tiệm cận ngang: y = 2
Giao với các trục tọa độ: (0; 4) và (-1; 0)
Đồ thị:
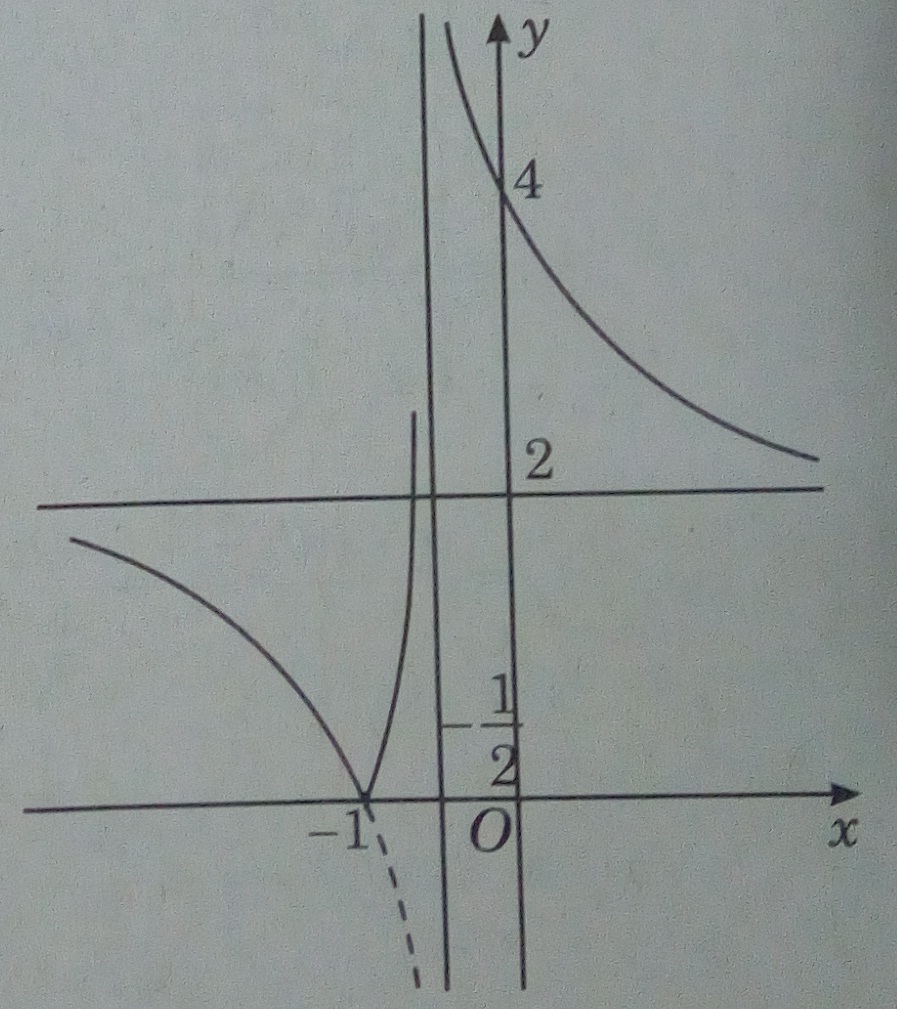
b) Đồ thị của hàm số được suy ra từ (C) bằng cách giữ nguyên phần đồ thị nằm phía trên trục hoành và lấy đối xứng qua trục hoành phần đồ thị nằm phía dưới trục hoành.
c) Tiếp tuyến có hệ số góc bằng \( – {1 \over 4}\).
Hoành độ tiếp điểm phải thỏa mãn phương trình \(- {4 \over {{{(2x + 1)}^2}}} = – {1 \over 4}\)
\(\Leftrightarrow {(2x + 1)^2} = 16\Leftrightarrow \left[ {\matrix{{x = – {5 \over 2}} \cr {x = {3 \over 2}} \cr} } \right.\)
Hai tiếp tuyến cần tìm là \(y = – {1 \over 4}x + {7 \over 8}\) và \(y = – {1 \over 4}x + {{23} \over 8}\).