Advertisements (Quảng cáo)
Chiếu một chùm ánh sáng trắng song song, hẹp coi như một tia sáng SI, vào một bể đựng nước với độ sâu 1 m với góc tới \({60^o}.\) Dưới đáy bể có một gương phẳng đặt song song với mặt nước. Tính chiều rộng của dãy màu mà ta thu được ở chùm sáng ló ra khỏi mặt nước. Cho biết chiết suất của nước đối với ánh sáng tím và ánh sáng đỏ là \({n_t} = 1,34;\,\,{n_đ} = 1,33.\)
Giải
Kí hiệu \({II_t},{J_t}{R_t}\) và \({II_đ},{J_đ}{R_đ}\) là các đường đi của tia tím và tia đỏ trong chùm sáng, i là góc tới, \({r_t}\) và \({r_đ}\) là góc khúc xạ của tia tím và tia đỏ , h là độ sâu của lớp nước trong bể (HÌnh 6.1G). Theo hình vẽ ta có:
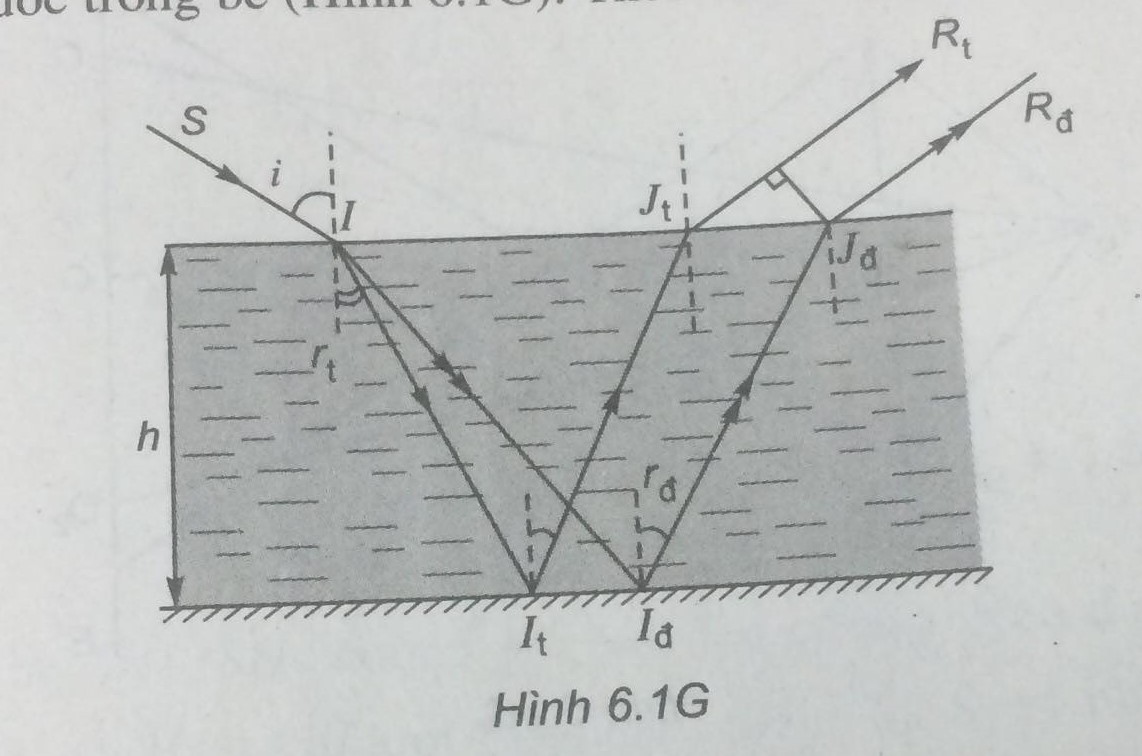
\(I{J_t} = 2h\tan {r_t};\,\,I{J_đ} = 2h\tan {r_đ}\)
Từ đó: \({J_t}{J_đ} = 2h\left( {\tan {r_đ}-\tan {r_t}} \right)\)
Kí hiệu a là bề rộng của dải màu khi ló ra không khí, ta có:
Advertisements (Quảng cáo)
\(a = {J_t}{J_đ}\cos i = 2h\cos i\left( {\tan {r_đ}-\tan {r_t}} \right)\)
Áp dụng định luật khúc xạ: \(\sin i = {n_đ}{{\mathop{\rm sinr}\nolimits} _đ};\,\sin i = {n_t}{{\mathop{\rm sinr}\nolimits} _t}\,\), ta tìm được:
\(\eqalign{ & {{\mathop{\rm tanr}\nolimits} _đ} = {{\sin {r_đ}} \over {\sqrt {1 – {{\sin }^2}{r_đ}} }} \approx 0,858 \cr & {{\mathop{\rm tanr}\nolimits} _t} = {{\sin {r_t}} \over {\sqrt {1 – {{\sin }^2}{r_t}} }} \approx 0,847 \cr} \)
Từ đó, ta tính được \(a \approx 11mm\)