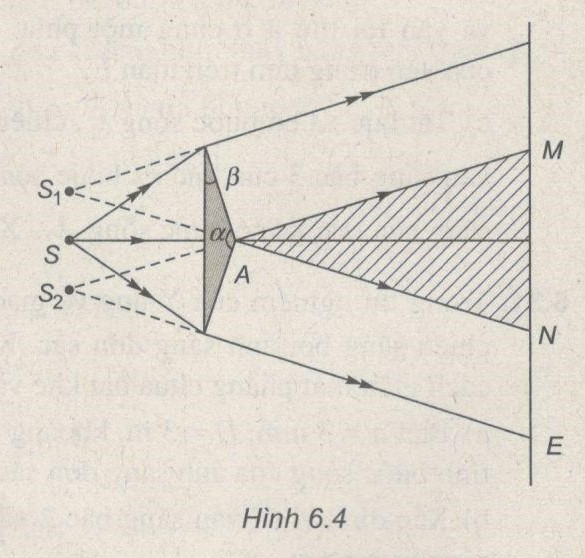
Để xác định được độ lớn của một góc rất tù \(\alpha \) (gần bằng \({180^0}\) ) của một lăng kính, người ta bố trí sơ đồ giao thoa như Hình 6.4. Bức xạ đơn sắc có bước sóng \({\lambda _1} = 0,633\,\mu m\) được rọi lên khe hẹp S tạo ra chùm sáng phân kì sau khe, chùm này rọi lên đáy lăng kính. Trong khoảng MN = 3,8 mm trên màn đặt cách lăng kính một khoảng d = 1,20 m có 8 vân tối và chính tại M , N là vân sáng.
a) Giải thích hiện tượng.
b) Tính góc \(\alpha \) của lăng kính, biết khe S cách lăng kính một khoảng d’ = 30,0 cm. Chiết suất của thủy tinh ứng với \({\lambda _1}\) là \({n_1} = 1,50.\)
c) Giữ nguyên cách bố trí thí nghiệm, rọi lên khe S chùm sáng đơn sắc \({\lambda _2} = 0,515\mu m\) thì thu được hệ vân có khoảng vân \({i_2} = 0,35\,mm\) . Xác định chiết suất \({n_2}\) của thủy tinh làm lăng kính đối với bức xạ này.
Giải
a) Giải thích hiện tượng: Độc giải tự lập luận
b) Theo đề bài thì khoảng MN chứa 8 khoảng vân, ta có:
Advertisements (Quảng cáo)
\({i_1} = {{MN} \over 8} = {{3,8} \over 8} = 0,475mm\)
Từ \({S_1}{S_2} = 2d’\left( {{n_1} - 1} \right)\beta = {{{\lambda _1}D} \over {{i_1}}}\) với \(D = d + d’ = 1,5m\) , ta được:
\(\beta = {{{\lambda _1}D} \over {2d’\left( {{n_1} - 1} \right){i_1}}} \Rightarrow \beta = 0,00666\,\,rad \approx 22,6’\)
Do đó: \(\alpha = {180^o} - 2\beta \approx {179^o}15’\)
c) Vì \(\beta ,d,D\) giữa nguyên không đổi, nên tương tự như câu b) ta có:
\(\beta = {{{\lambda _2}D} \over {2d’\left( {{n_2} - 1} \right){i_2}}}\)
Từ đó suy ra:
\(\eqalign{ & {{\left( {{n_2} - 1} \right){i_2}} \over {\left( {{n_1} - 1} \right){i_1}}} = {{{\lambda _2}} \over {{\lambda _1}}} \cr & {n_2} - 1 = \left( {{n_1} - 1} \right).{{{\lambda _2}} \over {{\lambda _1}}}.{{{i_1}} \over {{i_2}}} \approx 0,55 \Rightarrow {n_2} = 1,55 \cr} \)
