Advertisements (Quảng cáo)
Một thấu kính hội tụ mỏng có tiêu cự f = 50 cm được cắt ra làm hai phần bằng nhau theo mặt phẳng qua trục chính và vuông góc với tiết diện thấu kính. Một nguồn sáng điểm S phát ánh sáng đơn sắc đặt trên trục chính và cách thấu kính một khoảng d = 1,0 m (Hình 6.3).
a) Phải tách hai nửa thấu kính này ra đến khoảng cách nào (một cách đối xứng qua trục chính) để nhận được hai ảnh \({S_1},{S_2}\) cách nhau 4,0 mm.
b) Đặt một màn quan sát E vuông góc với trục chính và cách các ảnh \({S_1},{S_2}\) một khoảng D = 3,0 m. Tìm độ rộng của miền giao thoa trên màn E. Người ta đo được khoảng cách từ vân sáng trung tâm đến vân sáng bậc 8 là 3,2 mm. Tìm bước sóng của ánh sáng.
Giải
a) Ảnh của S tạo bởi thấu kính được xác định theo công thức:
\(d’ = {{df} \over {d – f}} = {{1.0,5} \over {1 – 0,5}} = 1m = 100cm\)
Do tách thấu kính ra hai nửa nên ta có hai ảnh thật \({S_1},{S_2}\) của S tạo bởi hai nửa thấu kính, hai ảnh này cũng cách thấu kính một khoảng d = 1m (Hình 6.2G). Từ các tam giác đồng dạng (đặt \({S_1}{S_2} = a\)), ta có:
\({b \over a} = {d \over {d + d’}} = {1 \over 2}\)
Khoảng cách xa của hai nửa thấu kính là: \(b = {a \over 2} = {4 \over 2} = 2,0mm\)
Advertisements (Quảng cáo)
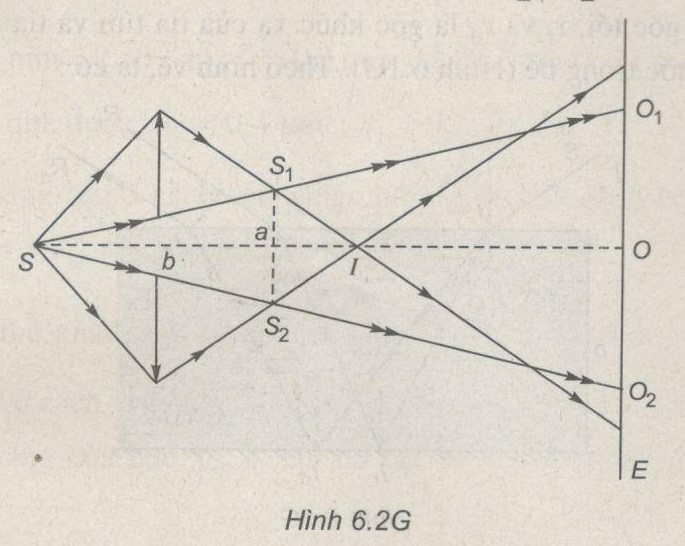
b) Hai chùm sáng khúc xạ qua hai nửa thấu kính giao nhau tạo miền \(I{O_1}{O_2}\) , tạo nên miền giao thoa \({O_1}{O_2}\) trên mà E (\({S_1}\) và \({S_2}\) được xem là hai nguồn kết hợp). Cũng từ các tam giác đồng dạng trên hình 6.2G, ta có:
\({b \over {{O_1}{O_2}}} = {d \over {d + d’ + D}} = {1 \over 5} \Rightarrow {O_1}{O_2} = 5b = 10mm\)
Theo để bài, ta có:
\(8i = 3,2mm \Rightarrow i = {{3,2} \over 8} = 0,4mm\)
Suy ra bước sóng \(\lambda \) :
\(\lambda = {{ia} \over D} \approx 0,53\mu m\)