Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) được thống kê lại như sau:
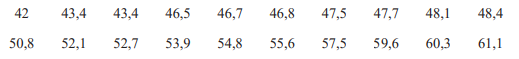a) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên. b) Hãy lập bảng tần số ghép nhóm với nhóm đầu tiên là [42; 46) và độ dài mỗi nhóm bằng 4. c) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm.
a) Khoảng biến thiên của mẫu số liệu là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu
Tìm trung vị \({Q_2}\)
Tìm trung vị của nửa số liệu bên trái \({Q_2}\), ta được \({Q_1}\)
Tìm trung vị của nửa số liệu bên phải \({Q_2}\), ta được \({Q_3}\)
Khoảng tứ phân vị của mẫu số liệu là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu
Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
c) Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Tính giá trị đại diện
Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
Advertisements (Quảng cáo)
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
a) Khoảng biến thiên của mẫu số liệu: 61,1 – 42 = 19,1 (km/h)
Cỡ mẫu: n = 20
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{20}}\) là mẫu số liệu gốc về tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ được xếp theo thứ tự không giảm.
Trung vị \({Q_2} = \frac{1}{2}({x_{10}} + {x_{11}}) = \frac{1}{2}(48,4 + 50,8) = 49,6\)
Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái \({Q_2}\) \({Q_1} = \frac{1}{2}({x_5} + {x_6}) = \frac{1}{2}(46,7 + 46,8) = 46,75\)
Tứ phân vị thứ ba là trung bị của nửa số liệu bên phải \({Q_2}\): \({Q_3} = \frac{1}{2}({x_{15}} + {x_{16}}) = \frac{1}{2}(54,8 + 55,6) = 55,2\)
Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} = {Q_3} - {Q_1} = 8,45\)
Số trung bình: \(\overline x = \frac{{42 + 43,4 + ... + 61,1}}{{20}} = 50,945\)
Phương sai: \({S^2} = \frac{{{{42}^2} + 43,{4^2} + ... + 61,{1^2}}}{{20}} - 50,{945^2} \approx 32,2\)
Độ lệch chuẩn: \(\sigma = \sqrt {32,2} \approx 5,67\)
b)
c) Ta có: \({x_1};...;{\rm{ }}{x_3} \in [42;46)\); \({x_4}; \ldots ;{\rm{ }}{x_{10}} \in [46;50)\);\({x_{11}}; \ldots ;{\rm{ }}{x_{14}} \in [50;54)\);\({x_{15}}; \ldots ;{\rm{ }}{x_{17}} \in [54;58)\);\({x_{18}};...;{x_{20}} \in [58;62)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_5} + {x_6}) \in [46;50)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}’ = 46 + \frac{{\frac{{20}}{4} - 3}}{7}(50 - 46) = \frac{{330}}{7}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{15}} + {x_{16}}) \in [54;58)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}’ = 54 + \frac{{\frac{{3.20}}{4} - (3 + 7 + 4)}}{3}(58 - 54) = \frac{{166}}{3}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}’ = {Q_3}’ - {Q_1}’ = \frac{{172}}{{21}}\)
Số trung bình: \(\overline x = \frac{{3.44 + 7.48 + 4.52 + 3.56 + 3.60}}{{20}} = 41,8\)
Phương sai: \({S^2} = \frac{{{{3.44}^2} + {{7.48}^2} + {{4.52}^2} + {{3.56}^2} + {{3.60}^2}}}{{20}} - 41,{8^2} = 364,96\)
Độ lệch chuẩn: \(\sigma = \sqrt {364,96} = 19,1\)