Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau:
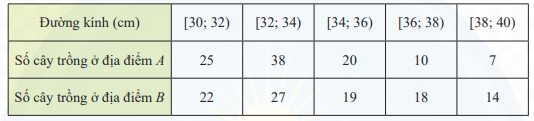a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B. b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?
a) Tính giá trị đại diện
Số trung bình: \(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\)
b) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x \) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Advertisements (Quảng cáo)
a)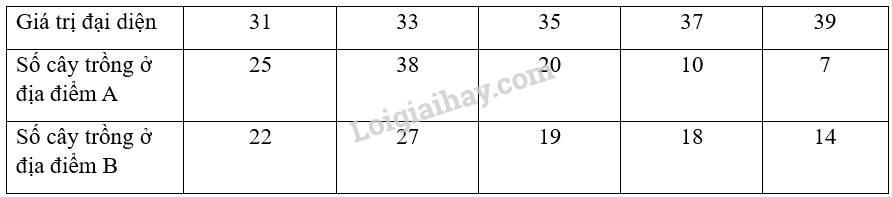
- Xét mẫu số liệu của địa điểm A:
Số trung bình: \({\overline x _A} = \frac{{25.31 + 38.33 + 20.35 + 10.37 + 7.39}}{{100}} = 33,72\)
- Xét mẫu số liệu của địa điểm B:
\({\overline x _B} = \frac{{22.31 + 27.33 + 19.35 + 18.37 + 14.39}}{{100}} = 34,5\)
Đường kính trung bình của thân cây xoan đào trồng tại địa điểm A nhỏ hơn tại địa điểm B.
b) - Xét mẫu số liệu của địa điểm A:
\({\sigma _A} = \sqrt {\frac{{{{25.31}^2} + {{38.33}^2} + {{20.35}^2} + {{10.37}^2} + {{7.39}^2}}}{{100}} - 33,{{72}^2}} = 2,32\)
- Xét mẫu số liệu của địa điểm B:
\({\sigma _B} = \sqrt {\frac{{{{22.31}^2} + {{27.33}^2} + {{19.35}^2} + {{18.37}^2} + {{14.39}^2}}}{{100}}} = 2,7\)
Vậy cây trồng tại địa điểm A có đường kính đồng đều hơn