
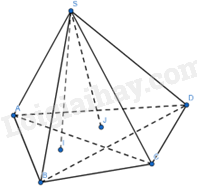
Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC. Chứng minh rằng \(2\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + \overrightarrow {SD} = 3(\overrightarrow {SI} + \overrightarrow {SJ} )\)

Áp dụng tính chất trọng tâm của tam giác và quy tắc 3 điểm

Xét S.ABC: \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SI} + \overrightarrow {IA} + \overrightarrow {SB} + \overrightarrow {IB} + \overrightarrow {SC} + \overrightarrow {IC} = 3\overrightarrow {SI} + (\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} )\)
Advertisements (Quảng cáo)
Vì I là trọng tâm tam giác ABC nên \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)
=> \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SI} \)
Xét S.ACD: \(\overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SJ} + \overrightarrow {JA} + \overrightarrow {SJ} + \overrightarrow {JC} + \overrightarrow {SJ} + \overrightarrow {JD} = 3\overrightarrow {SJ} + (\overrightarrow {JA} + \overrightarrow {JC} + \overrightarrow {JD} )\)
Vì J là trọng tâm tam giác ABC nên \(\overrightarrow {JA} + \overrightarrow {JC} + \overrightarrow {JD} = \overrightarrow 0 \)
=> \(\overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SD} = 3\overrightarrow {SJ} \)
Ta có: \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SD} = 3\overrightarrow {SI} + 3\overrightarrow {SJ} \Leftrightarrow 2\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + \overrightarrow {SD} = 3(\overrightarrow {SI} + \overrightarrow {SJ} )\)
