Câu hỏi/bài tập:

a) \(y = - {x^3} + 3x - 6\)
b) \(y = \frac{{x - 1}}{{x + 2}}\)
c) \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\)
d) \(y = \frac{{3x}}{{{x^2} - 9}}\)

Bước 1: Tính \(y’\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định hàm số đồng biến, nghịch biến trên khoảng nào và tìm cực trị của hàm số

a) \(y = - {x^3} + 3x - 6\)
Hàm số xác định trên R
Ta có: \(y’ = - 3{x^2} + 3\)
Xét \(y’ = 0\) \( \Rightarrow - 3{x^2} + 3 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Từ đó ta có bảng biến thiên là
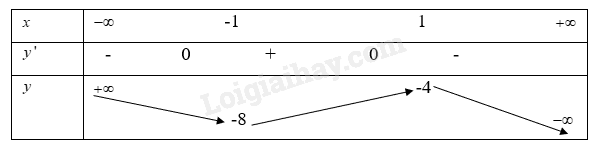
Từ bảng biến thiên ta có:
Hàm số \(y = - {x^3} + 3x - 6\) đồng biến trên khoảng\(( - 1;1)\)
Hàm số \(y = - {x^3} + 3x - 6\) nghịch biến trên khoảng\(( - \infty ; - 1),(1; + \infty )\)
Hàm số \(y = - {x^3} + 3x - 6\) đạt giá trị cực đại \(x = 1\)tại khi đó\(y = - 4\)
Hàm số \(y = - {x^3} + 3x - 6\) đạt giá trị cực tiểu tại \(x = - 1\) khi đó\(y = - 8\)
b) \(y = \frac{{x - 1}}{{x + 2}}\)
Advertisements (Quảng cáo)
Hàm số trên xác định trên R/{2}
Ta có: \(y’ = \frac{3}{{{{(x + 2)}^2}}}\)
Vì \(y’ = \frac{3}{{{{(x + 2)}^2}}} > 0\)với \(\forall x \in R/\{ - 2\} \)
Nên hàm số \(y = \frac{{x - 1}}{{x + 2}}\) đồng biến trên khoảng \(( - \infty ;2),(2; + \infty )\)
Và hàm số \(y = \frac{{x - 1}}{{x + 2}}\) không có điểm cực trị
c) \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\)
Hàm số xác định trên R/{-1}
Ta có: \(y’ = \frac{{( - 2x + 2)(x + 1) - ( - {x^2} + 2x + 2)}}{{{{(x + 1)}^2}}}\)
\( = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\)
Xét \(y’ = 0\)\( \Rightarrow - {x^2} - 2x = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\)
Từ đó ta có bảng biến thiên là
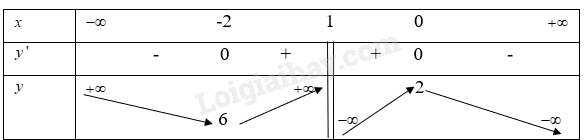
Từ bảng biến thiên, ta có:
Hàm số \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\) đồng biến trên khoảng\(( - 2;1),(1;2)\)
Hàm số \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\) nghịch biến trên khoảng\(( - \infty ; - 2),(0; + \infty )\)
Hàm số \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\) đạt giá trị cực đại \(x = 0\) tại khi đó \(y = 2\)
Hàm số \(y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}\) đạt giá trị cực tiểu tại \(x = - 2\) khi đó \(y = 6\)
d) \(y = \frac{{3x}}{{{x^2} - 9}}\)
Hàm số trên xác định trên R/{-3;3}
Ta có: \(y’ = \frac{{3({x^2} - 9) - 3x.2x}}{{{{({x^2} - 9)}^2}}}\) \( = \frac{{ - 3{x^2} - 27}}{{{{({x^2} - 9)}^2}}}\)
Vì \(y’ = \frac{{ - 3{x^2} - 27}}{{{{({x^2} - 9)}^2}}} < 0\) với \(\forall x \in R/\{ - 3;3\} \)
Nên hàm số \(y = \frac{{3x}}{{{x^2} - 9}}\) nghịch biến trên khoảng\(( - \infty ; - 3),( - 3;3),(3; + \infty )\)
Và hàm số\(y = \frac{{3x}}{{{x^2} - 9}}\) không có cực trị
