
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G, G’ lần lượt là trọng tâm các tam giác ABC và A’B’C’. O là giao điểm của hai đường thẳng AB’ và A’B.
a) Chứng minh rằng các đường thẳng GO và CG’ song song với nhau.
b) Tính độ dài của \(\overrightarrow {GO} \)trong trường hợp ABC.A’B’C’ là hình lăng trụ đứng, cạnh bên AA’ = 3 và đáy là tam giác đều có cạnh bằng 2.

- Tìm k (k≠0) sao cho \(\overrightarrow {GO} = k\overrightarrow {CG’} \) thì hai đường thẳng GO // CG’ bằng quy tắc trọng tâm tam giác và quy tắc trung điểm của vectơ.
- Tính độ dài của \(\overrightarrow {CG’} \) rồi suy ra độ dài của \(\overrightarrow {GO} \).

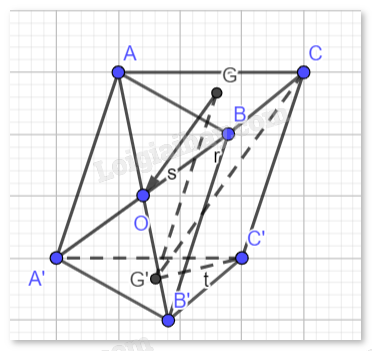
Hình bình hành AA’B’B có O là giao điểm của hai đường chéo nên O là trung điểm của AB’. Do đó: \(2\overrightarrow {GO} = \overrightarrow {GA} + \overrightarrow {GB’} = \overrightarrow {GA} + \overrightarrow {GG’} + \overrightarrow {G’B’} \).
Advertisements (Quảng cáo)
Vì ABC.A’B’C’ là hình lăng trụ có G, G’ lần lượt là trọng tâm của hai đáy nên: \(\overrightarrow {G’B’} = \overrightarrow {GB} ,\overrightarrow {GG’} = \overrightarrow {CC’} ,\overrightarrow {G’C’} = \overrightarrow {GC} \).
Suy ra: \(2\overrightarrow {GO} = \overrightarrow {GA} + \overrightarrow {CC’} + \overrightarrow {GB} = \overrightarrow {GA} + \overrightarrow {CG’} + \overrightarrow {G’C’} + \overrightarrow {GB} = \overrightarrow {GA} + \overrightarrow {CG’} + \overrightarrow {GC} + \overrightarrow {GB} \).
Áp dụng quy tắc trọng tâm của vectơ vào tam giác ABC, ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
Suy ra: \(2\overrightarrow {GO} = \left( {\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GB} } \right) + \overrightarrow {CG’} = \overrightarrow 0 + \overrightarrow {CG’} = \overrightarrow {CG’} \).
Vì tồn tại \(k = \frac{1}{2} \ne 0\) nên GO và CG’ song song với nhau.
b)
Vì ABC.A’B’C’ là hình lăng trụ là lăng trụ đứng nên tam giác CC’G’ vuông tại C’, ta có: \(CG’ = \sqrt {CC{‘^2} + C’G{‘^2}} \).
Mà G’ là trọng tâm của tam giác đều A’B’C’ nên: \(C’G’ = \frac{2}{3}.\frac{{\sqrt 3 }}{2}.2 = \frac{{2\sqrt 3 }}{3}\).
Suy ra: \(CG’ = \sqrt {{3^2} + {{\left( {\frac{{2\sqrt 3 }}{3}} \right)}^2}} = \frac{{\sqrt {93} }}{3}\).
Từ câu a ta thấy \(\overrightarrow {GO} = \frac{1}{2}\overrightarrow {CG’} \) nên \(\left| {\overrightarrow {GO} } \right| = \frac{1}{2}\left| {\overrightarrow {CG’} } \right| = \frac{1}{2}.\frac{{\sqrt {93} }}{3} = \frac{{\sqrt {93} }}{6}\).
