Câu hỏi/bài tập:
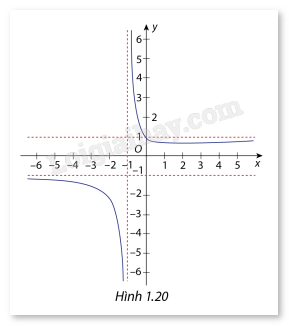
Cho hàm số \(y = f(x) = \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}\) có đồ thị là đường cong như hình 1.20. Hãy xác nhận các đường tiệm cận đứng và đường tiệm cận ngang của hàm số đã cho.

Xét \(f(x).\)
Advertisements (Quảng cáo)

Ta có \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = - \infty \;\), \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = + \infty \;\)
Suy ra x = - 1 là đường tiệm cận đứng của hàm số.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } f(x)\; = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\), \(\mathop {\lim }\limits_{x \to - \infty } f(x)\; = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\)
Suy ra y = 1 là đường tiệm cận ngang của hàm số.
