Câu hỏi/bài tập:
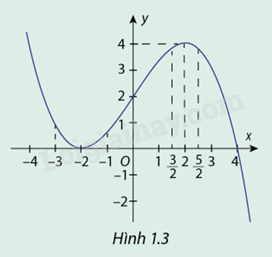
Hàm số \(y = f(x) = - \frac{1}{8}{x^3} + \frac{3}{2}x + 2\) có đồ thị cho ở hình 1.3
a) Giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị, só sánh \(f( - 2)\) với các giá trị khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, só sánh \(f(2)\) với các giá trị khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)

a) Tính \(f'(x)\) rồi giải phương trình \(f'(x) = 0\)
Advertisements (Quảng cáo)
b) Dựa vào đồ thị hàm số rồi giải

a) Ta có: \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2}\)
Xét \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2} = 0\)
\( \Rightarrow {x^2} = 4\)
\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
b) Dựa vào đồ thị, giá trị của \(f( - 2)\) luôn bé hơn các giá trị \(f(x)\) khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, giá trị của \(f(2)\)luôn lớn hơn các giá trị\(f(x)\) khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
