Bước 1: tính đạo hàm \(y’\). Hướng dẫn giải Câu hỏi Luyện tập 2 trang 5 SGK Toán 12 Kết nối tri thức - Bài 1. Tính đơn điệu và cực trị của hàm số.
Câu hỏi/bài tập:
Xét tính đơn điệu của hàm số \(y = \sin x - x\)trên khoảng \(( - \pi ;\pi )\)

Bước 1: tính đạo hàm \(y’\)
Bước 2: xét dấu \(y’\) rồi lập bảng biến thiên
Bước 3: Từ bảng biến thiên nhận xét tính đơn điệu của hàm số

Advertisements (Quảng cáo)
Hàm số đã cho xác định trên
Ta có: \(y’ = \cos x - 1\)
Vì \(\cos x \le 1\)với \(\forall x \in R\)
Nên \(y’ \le 0\)với \(\forall x \in R\)và \(y’ = 0\)tại \(x = 0\)
Khi đó ta có bảng biến thiên:
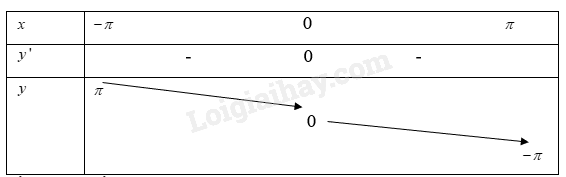
Vậy hàm số nghịch biến trên khoảng \(( - \pi ;\pi )\)
