Câu hỏi/bài tập:
Lập bảng biến thiên và kết luận các khoảng đồng biến, nghịch biến của hàm số.
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)

Bước 1: Xét \(f'(x) = 0\)qua đó tìm x
Bước 2: Xét dấu \(f'(x)\)
Bước 3: lập bảng biến thiên

a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
Hàm số trên xác định trên R\ {-3}
Ta có: \(f'(x) = \frac{{2(x + 3) - (2x - 1)}}{{{{(x + 3)}^2}}}\)
\(f'(x) = \frac{7}{{{{(x + 3)}^2}}}\)
Vì \(f'(x) > 0\)với \(\forall x \ne - 3\) từ đó ta có bảng biến thiên
Advertisements (Quảng cáo)
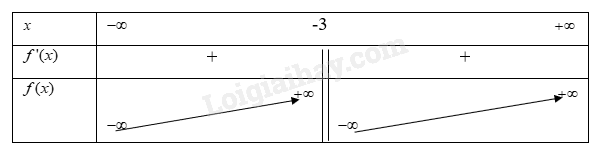
Từ bảng biến thiên ta có,
Hàm số \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\) đồng biến trên khoảng \(( - \infty ; - 3)\)và \(( - 3; + \infty )\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Hàm số trên xác định trên R
Ta có \(y = f'(x) = - \sin x\)
Xét \(f'(x) = - \sin x = 0\) \( \Rightarrow x = k\pi \)
Mà \(x \in (0;2\pi )\) \( \Rightarrow x = \pi \)
Khi đó ta có bảng biến thiên
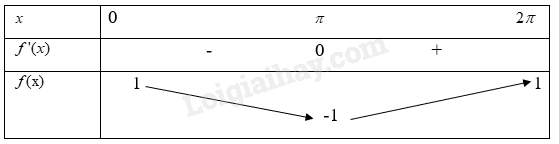
Từ bảng biến thiên ta có
Hàm số \(f(x) = \cos x\) đồng biến trên khoảng\((\pi ;2\pi )\)
Hàm số \(f(x) = \cos x\) nghịch biến trên khoảng\((0;\pi )\)
