Hoạt động (HĐ) 3
Trong không gian Oxyz, cho hai vectơ \(\vec a = ({x_1},{y_1},{z_1})\) và \(\vec b = ({x_2},{y_2},{z_2})\).
a) Biểu diễn \(\vec a\) và \(\vec b\) qua các vectơ đơn vị \(\vec i,\vec j,\vec k\).
b) Tính \(\vec a \cdot \vec b\).

- Sử dụng định nghĩa toạ độ của một vectơ trong một hệ toạ độ để biểu diễn \(\vec a\) và \(\vec b\)
- Sử dụng kết quả của câu a và tính chất của các vectơ đơn vị \(\vec a \cdot \vec b\).

a) Biểu diễn vectơ
\(\vec a = {x_1}\vec i + {y_1}\vec j + {z_1}\vec k\)
\(\vec b = {x_2}\vec i + {y_2}\vec j + {z_2}\vec k\)
b) Tính \(\vec a \cdot \vec b\).
Từ câu a ta có:
\(\begin{array}{l}\overrightarrow a .\overrightarrow b = \left( {{x_1}\vec i + {y_1}\vec j + {z_1}\vec k} \right).\left( {{x_2}\vec i + {y_2}\vec j + {z_2}\vec k} \right)\\\overrightarrow a .\overrightarrow b = {x_1}\vec i\left( {{x_2}\vec i + {y_2}\vec j + {z_2}\vec k} \right) + {y_1}\vec j\left( {{x_2}\vec i + {y_2}\vec j + {z_2}\vec k} \right) + {z_1}\vec k\left( {{x_2}\vec i + {y_2}\vec j + {z_2}\vec k} \right)\end{array}\)(*)
Sử dụng các tính chất của các vectơ đơn vị ta có:
\(\overrightarrow i .\overrightarrow i = 1,\overrightarrow j .\overrightarrow j = 1,\overrightarrow k .\overrightarrow k = 1,\overrightarrow i .\overrightarrow k = 0,\overrightarrow i .\overrightarrow j = 0,\overrightarrow k .\overrightarrow j = 0\)
Tính từng phần trong (*):
\({x_1}\left( {\vec i \cdot \left( {{x_2}\vec i + {y_2}\vec j + {z_2}\vec k} \right)} \right) = {x_1}\left( {{x_2}(\vec i \cdot \vec i) + {y_2}(\vec i \cdot \vec j) + {z_2}(\vec i \cdot \vec k)} \right) = {x_1}{x_2}\)
\({y_1}\left( {\vec j \cdot \left( {{x_2}\vec i + {y_2}\vec j + {z_2}\vec k} \right)} \right) = {y_1}\left( {{x_2}(\vec j \cdot \vec i) + {y_2}(\vec j \cdot \vec j) + {z_2}(\vec j \cdot \vec k)} \right) = {y_1}{y_2}\)
\({z_1}\left( {\vec k \cdot \left( {{x_2}\vec i + {y_2}\vec j + {z_2}\vec k} \right)} \right) = {z_1}\left( {{x_2}(\vec k \cdot \vec i) + {y_2}(\vec k \cdot \vec j) + {z_2}(\vec k \cdot \vec k)} \right) = {z_1}{z_2}\)
Cộng tất cả các phần lại:
\(\overrightarrow a .\overrightarrow b = {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}\)
Luyện tập (LT) 4
Trong không gian Oxyz, hình chóp S.ABC có S(3;1;3), A(2;3;1), B(4;3;3), C(2;3;1). M là trung điểm của BC. Tính góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SM} \).

- Tìm tọa độ các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SM} \)
- Tính tích vô hướng \(\overrightarrow {AB} \cdot \overrightarrow {SM} \)
- Tính độ dài của các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SM} \)
- Tính góc giữa hai vectơ

- Vectơ \(\overrightarrow {AB} \):
\(\overrightarrow {AB} = B - A = (4 - 2;3 - 3;3 - 1) = (2;0;2)\)
- Tọa độ của điểm M là trung điểm của BC:
\(M = \left( {\frac{{4 + 2}}{2};\frac{{3 + 3}}{2};\frac{{3 + 1}}{2}} \right) = (3;3;2)\)
- Vectơ \(\overrightarrow {SM} \):
\(\overrightarrow {SM} = M - S = (3 - 3;3 - 1;2 - 3) = (0;2; - 1)\)
- Tích vô hướng \(\overrightarrow {AB} \cdot \overrightarrow {SM} \)
\(\overrightarrow {AB} \cdot \overrightarrow {SM} = 2 \times 0 + 0 \times 2 + 2 \times ( - 1) = - 2\)
- Độ dài của vectơ \(\overrightarrow {AB} \):
\(|\overrightarrow {AB} | = \sqrt {{2^2} + {0^2} + {2^2}} = \sqrt 8 = 2\sqrt 2 \)
- Độ dài của vectơ \(\overrightarrow {SM} \):
\(|\overrightarrow {SM} | = \sqrt {{0^2} + {2^2} + {{( - 1)}^2}} = \sqrt 5 \)
Tính góc giữa hai vectơ:
\(\cos \theta = \frac{{\overrightarrow {AB} \cdot \overrightarrow {SM} }}{{|\overrightarrow {AB} | \times |\overrightarrow {SM} |}} = \frac{{ - 2}}{{2\sqrt 2 \times \sqrt 5 }} = \frac{{ - 1}}{{\sqrt {10} }}\)
Vậy góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SM} \) là:
\(\theta = \arccos \left( {\frac{{ - 1}}{{\sqrt {10} }}} \right)\)
Luyện tập (LT) 5
Advertisements (Quảng cáo)
Trong không gian Oxyz, cho hình chóp S.ABC với
\(S\left( { - 2;1;3} \right),{\rm{ }}A\left( { - 4;3;2} \right),{\rm{ }}B\left( {0;2;1} \right),C\left( { - 2;1 + \sqrt 3 ;3} \right)\).
a) Chứng minh rằng hai cạnh bên SA, SB bằng nhau và vuông góc với nhau.
b) Tính số đo của \(\widehat {ASC}\) (làm tròn kết quả đến hàng phần trăm).

a) Sử dụng tính chất hai vectơ bằng nhau thì tích vô hướng của chúng bằng \(\overrightarrow 0 \).
b) Tìm cos của \(\widehat {ASC}\) từ tích vô hướng của hai vectơ \(\overrightarrow {SA} .\overrightarrow {SC} \) sau đó suy ra giá trị của \(\widehat {ASC}\)

Vectơ \(\overrightarrow {SA} \) có tọa độ:
\(\overrightarrow {SA} = A - S = ( - 4 - ( - 2),3 - 1,2 - 3) = ( - 2,2, - 1)\)
Độ dài của vectơ \(\overrightarrow {SA} \) là:
\(|\overrightarrow {SA} | = \sqrt {{{( - 2)}^2} + {2^2} + {{( - 1)}^2}} = \sqrt {4 + 4 + 1} = \sqrt 9 = 3\)
Vectơ \(\overrightarrow {SB} \) có tọa độ:
\(\overrightarrow {SB} = B - S = (0 - ( - 2),2 - 1,1 - 3) = (2,1, - 2)\)
Độ dài của vectơ \(\overrightarrow {SB} \) là:
\(|\overrightarrow {SB} | = \sqrt {{2^2} + {1^2} + {{( - 2)}^2}} = \sqrt {4 + 1 + 4} = \sqrt 9 = 3\)
Suy ra SA và SB bằng nhau.
Tích vô hướng của \(\overrightarrow {SA} \) và \(\overrightarrow {SB} \) là:
\(\overrightarrow {SA} \cdot \overrightarrow {SB} = ( - 2)(2) + 2(1) + ( - 1)( - 2) = - 4 + 2 + 2 = 0\)
\(\overrightarrow {SA} \cdot \overrightarrow {SB} = 0\), nên SA và SB vuông góc với nhau.
Tích vô hướng của \(\overrightarrow {SA} \) và \(\overrightarrow {SC} \) là:
\(\overrightarrow {SA} \cdot \overrightarrow {SC} = ( - 2)(0) + 2(\sqrt 3 ) + ( - 1)(0) = 2\sqrt 3 \)
Độ dài của vectơ \(\overrightarrow {SC} \) là:
\(|\overrightarrow {SC} | = \sqrt {{0^2} + {{(\sqrt 3 )}^2} + {0^2}} = \sqrt 3 \)
Góc giữa hai vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {SC} \) được tính bằng công thức:
\(\cos \widehat {ASC} = \frac{{\overrightarrow {SA} \cdot \overrightarrow {SC} }}{{|\overrightarrow {SA} | \cdot |\overrightarrow {SC} |}} = \frac{{2\sqrt 3 }}{{3 \cdot \sqrt 3 }} = \frac{{2\sqrt 3 }}{{3\sqrt 3 }} = \frac{2}{3}\)
Suy ra:
\(\widehat {ASC} = {\cos ^{ - 1}}\left( {\frac{2}{3}} \right)\)
Vận dụng (VD) 2
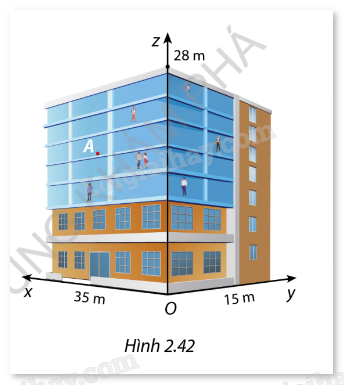
Một tòa nhà có dạng hình hộp chữ nhật với kích thước chiều dài 35 m, chiều rộng 15 m, chiều cao 28 m. Người ta định vị các vị trí trong tòa nhà dựa vào một hệ trục tọa độ Oxyz như Hình 2.42.
a) Chị Hương đang đứng ở vị trí A(20; 5; 20) và đi chuyển đến thang máy để xuống sảnh chờ đón khách. Biết vị trí vào thang máy có hoành độ x = 15 và tung độ y = 3. Hỏi chị Hương mất bao nhiêu giây để di chuyển, nếu từ vị trí A có thể đi thẳng đến cửa thang máy và chị ấy đi bộ với tốc độ 1,5 m/s?
b) Chị Hương vừa đặt một bộ phát sóng wifi trong phòng làm việc của mình tại vị trí có tọa độ (20; 5; 20). Do yêu cầu của công việc, sáng nay chị Hương phải đứng ở bàn lễ tân có tọa độ (5; 0; 0) để đón khách. Hỏi trong lúc đứng ở bàn lễ tân chờ khách thì điện thoại của chị có bắt được sóng wifi phát ra từ phòng làm việc của mình hay không? Biết rằng vùng phủ sóng bộ phát wifi nói trên có bán kính 30 mét.

a) Để tính thời gian chị Hương di chuyển từ vị trí A(20; 5; 20) đến vị trí thang máy, ta cần tính khoảng cách giữa hai điểm trong không gian Oxyz bằng công thức:
\(d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \)
Sau đó, thời gian di chuyển được tính bằng: \(t = \frac{d}{v}\) với v là tốc độ di chuyển.
b) Để kiểm tra xem chị Hương có thể bắt được sóng wifi hay không, ta cần tính khoảng cách giữa hai điểm (20; 5; 20) và (5; 0; 0), và so sánh với bán kính phủ sóng của bộ phát wifi.

a) Tính khoảng cách giữa điểm A(20; 5; 20) và vị trí thang máy (15; 3; 0):
\(d = \sqrt {{{(15 - 20)}^2} + {{(3 - 5)}^2} + {{(0 - 20)}^2}} = \sqrt {{{( - 5)}^2} + {{( - 2)}^2} + {{( - 20)}^2}} = \sqrt {25 + 4 + 400} = \sqrt {429} \approx 20.71{\rm{ m}}\)
Thời gian di chuyển:
\(t = \frac{{20.71}}{{1.5}} \approx 13.81 {\rm{ giây}}\)
b) Tính khoảng cách từ phòng làm việc (20; 5; 20) đến bàn lễ tân (5; 0; 0):
\(d = \sqrt {{{(20 - 5)}^2} + {{(5 - 0)}^2} + {{(20 - 0)}^2}} = \sqrt {{{15}^2} + {5^2} + {{20}^2}} = \sqrt {225 + 25 + 400} = \sqrt {650} \approx 25.5{\rm{ m}}\)
Vì khoảng cách này (25.5 m) nhỏ hơn bán kính phủ sóng của wifi (30 m), nên chị Hương có thể bắt được sóng wifi từ phòng làm việc.
