Hoạt động (HĐ) 3
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số \(y = f(x) = x + \frac{x}{{{x^2} - 1}}\) và đường thẳng \(\Delta :y = x\) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và\(\Delta \) có cùng hoành độ x, với x > 1 hoặc x
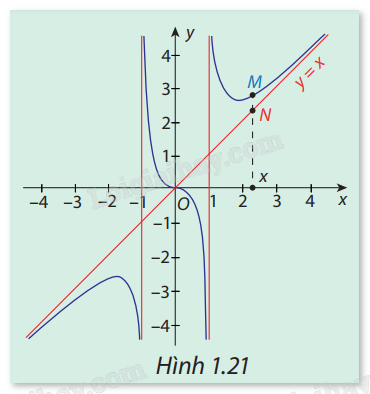

Nhìn vào đồ thị rồi nhận xét.

Khi \(x \to - \infty \) và \(x \to + \infty \) thì độ dài MN càng ngắn.
Luyện tập (LT) 3
Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\).

Phân tích hàm số rồi áp dụng ghi chú: hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận đứng \(x = - \frac{n}{m}\)là và đường tiệm cận xiên là \(y = px + q.\)

Ta có \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\)\( = - x - 2 - \frac{1}{{x + 1}}.\)
Áp dụng ghi chú hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận xiên là \(y = px + q\), khi đó đường tiệm cận xiên của hàm số là \(y = - x - 2.\)
Vận dụng (VD) 1
Trong phần Khởi động đầu bài, tìm đường tiệm cận đứng của đồ thị hàm số \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), từ đó nhận xét khối lượng của vật khi vận tốc của nó càng gần vận tốc ánh sáng.

Tìm giới hạn của khối lượng m(v) khi vận tốc v tiến gần đến tốc độ ánh sáng c.
Advertisements (Quảng cáo)

Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\).
Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \).
Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
\(\mathop {\lim }\limits_{v \to c - } m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to c - } \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số. Khi vận tốc của vật tiến dần đến tốc độ ánh sáng, khối lượng của vật càng lớn.
Vận dụng (VD) 2
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \(y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \(y = \frac{{40}}{{27}}x\) là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).
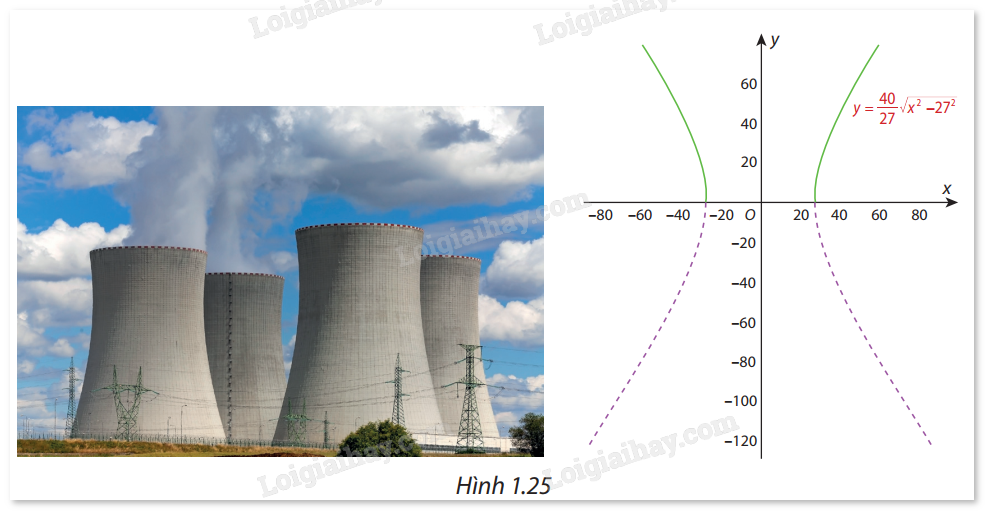

Chứng minh \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = 0\).

\(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{40}}{{27}}\left( {\sqrt {{x^2} - {{27}^2}} - x} \right)} \right] = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - {{27}^2}} - x} \right)\)
\( = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\frac{{{x^2} - {{27}^2} - {x^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\left( {\frac{{ - {{27}^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{\sqrt {{x^2} - {{27}^2}} + x}}\)
\( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{x\sqrt {1 - \frac{{{{27}^2}}}{{{x^2}}}} + x}} = 0.\)
Vậy \(y = \frac{{40}}{{27}}x\) là tiệm cận xiên của (C).
Tương tự, một tiệm cận xiên khác của (C) là \(y = - \frac{{40}}{{27}}x\).
